Giải bởi Vietjack
Lời giải:
Áp suất đáy ở mỗi nhánh bình thông nhau sẽ bằng nhau.
Khi chưa đặt quả cân lên, ta sẽ có:
\(\frac{{10{M_1}}}{{{S_1}}} + d.{h_1} = \frac{{10{M_2}}}{{{S_2}}} + d.{h_2}\)\( \Leftrightarrow \frac{{10{M_2}}}{{{S_2}}} - \frac{{10{M_1}}}{{{S_1}}} = d.({h_1} - {h_2}) = d.0,1\,\,(1)\)
Khi đặt quả cân 2 kg lên pittông 1: \(\frac{{10({M_1} + m)}}{{{S_1}}} = \frac{{10{M_2}}}{{{S_2}}}\)
Thay số tính được: \({S_2} = \frac{2}{3}{S_1}\)
Thay vào (1) được: \({S_1} = \frac{{200}}{{0,1.d}}\,\,(2)\)
Đặt quả cân 2 kg lên pittông thứ 2 ta sẽ có:
\(\frac{{10{M_1}}}{{{S_1}}} + d.{h_1}^' = \frac{{10({M_2} + m)}}{{{S_2}}} + d.{h_2}^'\)\( \Leftrightarrow \frac{{400}}{{{S_2}}} - \frac{{100}}{{{S_1}}} = d.\Delta H\)\( \Leftrightarrow \frac{{500}}{{{S_1}}} = d.\Delta H\)
\( \Rightarrow \Delta H = 25cm\)
Cho mạch điện như hình vẽ:
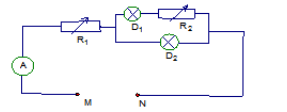
Đèn Đ1 loại 3 V - 1,5 W, đèn Đ2 loại 6 V - 3 W. Hiệu điện thế giữa hai điểm M và N là UMN = 9 V. Ampe kế A và dây nối có điện trở không đáng kể. Điều chỉnh cho R1 = 1,2 \[\Omega \] và R2 = 2 \[\Omega \]. Tìm số chỉ của ampe kế, các đèn sáng thế nào?
Ô tô có khối lượng 1200 kg khi chạy trên đường nằm ngang với vận tốc v = 72 km/h thì tiêu hao 80 g xăng trên đoạn đường S = 1 km. Hiệu suất động cơ là 20%.
Tính công suất của ô tô. Cho biết khi 1 kg xăng bị đốt cháy thì tỏa ra năng lượng là 45.106 J.
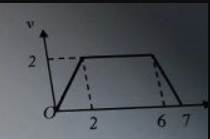
Khi ô tô đang chạy với vận tốc 15 m/s trên một đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy chậm dần đều. Sau khi chạy thêm 125 m thì vận tốc của ô tô chỉ còn 10 m/s. Hãy tính :
a) Gia tốc của ô tô.
b) Thời gian ô tô chạy thêm được 125 m kể từ khi bắt đầu hãm phanh.
c) Thời gian chuyển động cho đến khi xe dừng hẳn.
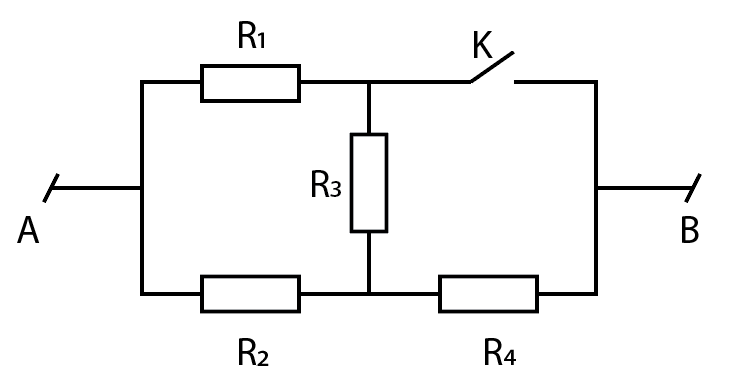
Cho mạch \[{R_1}nt\left( {\left( {{R_2}nt{R_3}} \right)//{R_4}} \right)\].
Biết \[{R_1} = 5\,\Omega ,{\rm{ }}{R_2} = 30\,\Omega ,{\rm{ }}{R_3} = {R_4} = 10\,\Omega \], r =2 \[\Omega \], E = 15 V.
a) Tìm nhiệt lượng toả ra trên \[{R_3}\] sau 3 phút 20 s.
b) Tìm UMN (M trước \[{R_1}\], N giữa \[{R_2}\] và \[{R_3}\]).
