Trắc nghiệm tổng hợp Vật lí 2023 có đáp án (Phần 8)
-
3261 lượt thi
-
53 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải:
Áp dụng định lí động năng khi vật rơi trong không khí
\[{W_{d\max }} - {W_{d1}} = {A_1} \Rightarrow \frac{1}{2}m{v^2} - 0 = P.{h_1} + F.{h_1}.\cos {180^0} \Rightarrow \frac{1}{2}m{v^2} = \left( {P - {F_1}} \right){h_1}\,\,\,\left( 1 \right)\]
Áp dụng định lí động năng từ khi chạm đất đến khi dừng lại trong đất:
\[{W_{d2}} - {W_{d\max }} = {A_2} \Rightarrow 0 - \frac{1}{2}m{v^2} = P.{h_2} + F.{h_2}.\cos {180^0} \Rightarrow \frac{1}{2}m{v^2} = \left( {{F_2} - P} \right){h_2}\,\,\,\left( 2 \right)\]
Từ (1) và (2):
\[\left( {P - {F_1}} \right){h_2} = \left( {{F_2} - P} \right){h_2} \Rightarrow {F_2} = \frac{{\left( {P - {F_1}} \right).{h_1}}}{{{h_2}}} + P = \frac{{\left( {100 - 40} \right).3}}{{0,3}} + 100 = 700\,N\]
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
\[BC = \sqrt {A{B^2} + A{C^2}} = 10\,cm \Rightarrow \cos \widehat B = \frac{{AB}}{{BC}}\]
\[{U_{BA}} = E.BA.\cos \widehat B = 4000.0,06.\frac{6}{{10}} = 144\,V\]
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
Bước sóng λ = v/T = 1,5.0,02 = 0,03 m = 3cm
- Phương trình sóng tới tại điểm B là uB = 2cos100πt mm
=> Phương trình sóng tới tại điểm M: uM = 2cos(100πt + 2π.0,5/3) mm
Hay uM = 2cos(100πt + π/3) mm
Phương trình sóng phản xạ tại điểm B là: u’B = 2cos(100πt + π) mm
=> Phương trình sóng phản xạ tại M là uM = 2cos(100πt + π - 2π.0,5/3) mm
Hay u’M = 2cos(100πt + 2π/3) mm
Phương trình sóng tổng hợp tại M là u = uM + u’M
\[u = 2.2\cos \left( {\frac{\pi }{6}} \right)\cos \left( {100\pi t - \frac{\pi }{2}} \right) = 2\sqrt 3 \cos \left( {100\pi t - \frac{\pi }{2}} \right)mm\]
Câu 5:
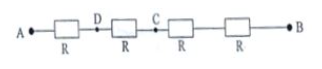
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án B
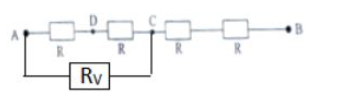
Khi vôn kế mắc vào A và C, \[{U_{CB}} = 132 - 44 = 88V\]
\[I = \frac{{{U_{CB}}}}{{2R}} = \frac{{44}}{R}\]
\[{R_{AC}} = \frac{{{U_{AC}}}}{I} = R = \frac{{2R.{R_V}}}{{2R + {R_V}}} \Rightarrow {R_V} = 2R\]
Khi vôn kế mắc vào A và D, \[{R_{AD}} = \frac{{R.{R_V}}}{{R + {R_V}}} = \frac{{R.2R}}{{R + 2R}} = \frac{{2R}}{3}\]
\[{R_{AB}} = \frac{{11R}}{3} \Rightarrow I = \frac{{{U_{AB}}}}{{{R_{AB}}}} = \frac{{36}}{R}\]\[ \Rightarrow {R_{AD}} = I.{R_{AD}} = 24V\]
Câu 6:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án B
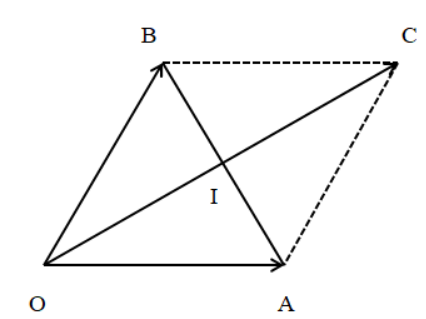
Đặt \[\overrightarrow {{F_1}} = \overrightarrow {OA} \] và \[\overrightarrow {{F_2}} = \overrightarrow {OB} \]. Khi đó ta có \[\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = 50\,\,(N)\] và \[\widehat {AOB} = 60^\circ \].
Dựng điểm C sao cho tứ giác OACB là hình bình hành.
Theo quy tắc hình bình hành, ta có: \[\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \] hay \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OC} \]
Suy ra lực tổng hợp của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] là \[\overrightarrow {OC} \].
Do đó cường độ tổng hợp lực của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] là \[\left| {\overrightarrow {OC} } \right|\]= OC.
Vì OA = OB và \[\widehat {AOB} = 60^\circ \] nên tam giác OAB đều, do đó: AB = OA = OB = 50.
Gọi I là giao điểm của OC và AB
⇒ I là trung điểm OC và AB ⇒ BI = \[\frac{{AB}}{2} = \frac{{\left| {\overrightarrow {AB} } \right|}}{2} = \frac{{50}}{2}\]= 25(N).
Tam giác OAB đều có OI là đường trung tuyến.
Suy ra OI cũng là đường cao của tam giác OAB.
Tam giác OBI vuông tại I: \[O{I^2} = O{B^2} - B{I^2}\] (Định lý Pytago)
\[ \Leftrightarrow O{I^2} = {50^2} - {25^2} = 1875\]
\[ \Rightarrow OI = 25\sqrt 3 (N)\]
Do đó OC = 2OI = \[50\sqrt 3 \] (N).
Câu 7:
Cho mạch \[{R_1}nt\left( {\left( {{R_2}nt{R_3}} \right)//{R_4}} \right)\].
Biết \[{R_1} = 5\,\Omega ,{\rm{ }}{R_2} = 30\,\Omega ,{\rm{ }}{R_3} = {R_4} = 10\,\Omega \], r =2 \[\Omega \], E = 15 V.
a) Tìm nhiệt lượng toả ra trên \[{R_3}\] sau 3 phút 20 s.
b) Tìm UMN (M trước \[{R_1}\], N giữa \[{R_2}\] và \[{R_3}\]).
 Xem đáp án
Xem đáp án
Lời giải:
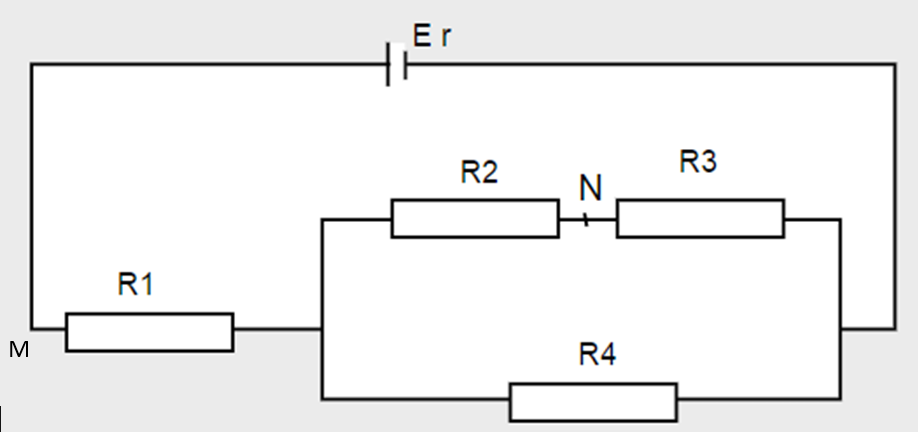
a.
\[{R_{23}} = {R_2} + {R_3} = 30 + 10 = 40\,\,\Omega \]
\[{R_{234}} = \frac{{40.10}}{{40 + 10}} = 8\,\,\Omega \]
Cường độ dòng điện mạch chính:
\[{U_{234}} = I.{R_{234}} = 1.8 = 8V\]
Cường độ dòng điện qua điện trở \[{R_3}\] là: \[{I_3} = \frac{{{U_{234}}}}{{{R_{23}}}} = \frac{8}{{40}} = 0,2A\]
Nhiệt lượng tỏa ra trên điện trở \[{R_3}\] sau 3 phút 20 s là:
\[Q = {I^2}.{R_3}.t = {0,2^2}.10.(3.60 + 20) = 80(J)\]
b. Hiệu điện thế: \[{U_{MN}} = {U_{MP}} + {U_{PN}} = {U_1} + {U_2}\] (P là điểm sau R1)
\[ \Rightarrow {U_{MN}} = {I_1}.{R_2} + {I_2}.{R_2} = 1.5 + 0,2.30 = 11(V)\]
Câu 8:
biến đổi chuyển động của vật chậm dần? Trọng lực là gì? Đơn vị đo của lực là gì?
 Xem đáp án
Xem đáp án
Lời giải:
- Lực có 2 tác dụng: Làm biến đổi chuyển động và làm biến dạng vật.
Chẳng hạn như: Khi ta đang đi xe đạp, nếu ta bóp phanh, tức là tác dụng lực cản vào xe đạp, thì xe đạp sẽ chuyển động chậm dần, rồi dừng lại.
- Trọng lực là lực hút của Trái Đất tác dụng lên vật và độ lớn của nó được gọi là trọng lượng.
- Đơn vị đo của lực là Niutơn (N).
Câu 9:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
- Lực là tác dụng đẩy, kéo của vật này lên vật khác.
- Lực tác dụng lên một vật có thể làm biến đổi chuyển động của vật hoặc làm cho vật bị biến dạng.
Câu 10:
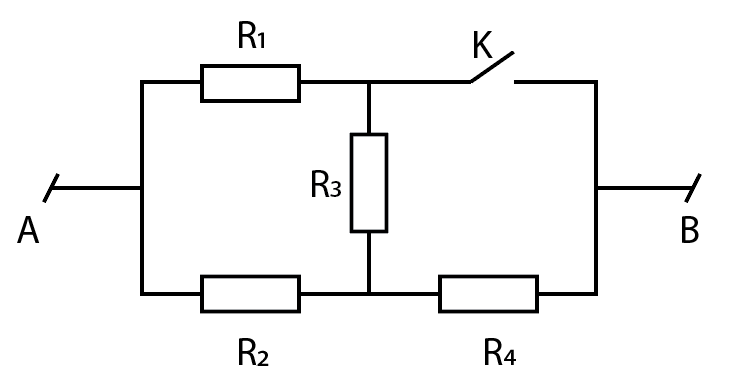
 Xem đáp án
Xem đáp án
Lời giải:
+ Khi K mở ta có sơ đồ:
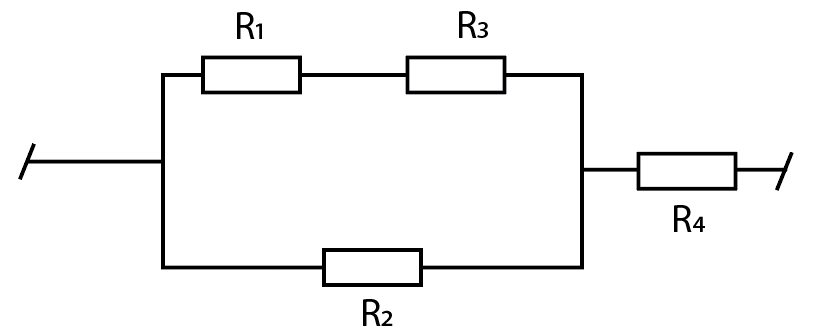
\[{R_{13}} = {R_1} + {R_3} = 45 + 45 = 90\Omega \]
\[{R_{123}} = \frac{{{R_{13}}.{R_2}}}{{{R_{13}} + {R_2}}} = \frac{{90.90}}{{90 + 90}} = 45\Omega \]
Điện trở tương đương toàn mạch là: \[R = {R_{123}} + {R_4} = 45 + {R_4}\]
Cường độ dòng điện qua \[{R_4}\]khi K mở là: \[{I_4} = \frac{U}{R} = \frac{{90}}{{45 + {R_4}}}\]
+ Khi K đóng ta có sơ đồ:
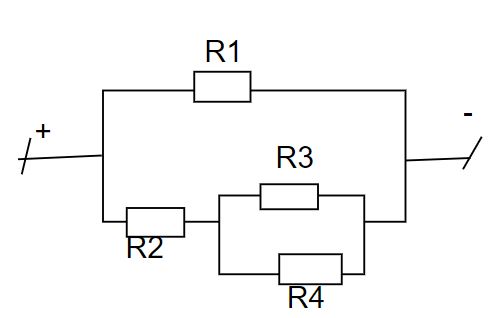
\[{R_{34}}\prime = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\]
\[{R_{234}}\prime = {R_2} + {R_{34}}\prime = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\]
Ta có: \[{U_{234}}' = U = 90V\]
\[ \Rightarrow {I_{234}}' = {I_2}' = {I_{34}}' = \frac{U}{{{R_{234}}}} = \frac{{90\left( {45 + {R_4}} \right)}}{{4050 + 135{R_4}}} = \frac{{4050 + 90{R_4}}}{{4050 + 135{R_4}}}\]
\[ \Rightarrow {U_2}^' = {I_2}^'{R_2} = \frac{{\left( {4050 + 90{R_4}} \right).90}}{{4050 + 135{R_4}}} = \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\]
\[ = > {U_4}' = {U_{34}}' = {U_{234}}' - {U_2}' = 90 - \frac{{364500 + 8100{R_4}}}{{4050 + 135{R_4}}}\] \[ = \frac{{364500 + 12150{R_4} - 364500 - 8100{R_4}}}{{4050 + 135{R_4}}} = \frac{{4050{R_4}}}{{4050 + 135{R_4}}}\]
\[ \Rightarrow {I_4}^' = \frac{{{U_4}^'}}{{{R_4}}} = \frac{{4050{R_4}}}{{{R_4}\left( {4050 + 135{R_4}} \right)}} = \frac{{4050}}{{4050 + 135{R_4}}}\]
Từ hai trường hợp K đóng và K mở trên suy ra:
\[{I_4} = {I_4}^' \Leftrightarrow \frac{{4050}}{{4050 + 135{R_4}}} = \frac{{90}}{{45 + {R_4}}}\]
\[ \Rightarrow 4050\left( {45 + {R_4}} \right) = 90\left( {4050 + 135{R_4}} \right)\]
\[ \Rightarrow {R_4} = - 22,5\,\Omega \] (loại). Không có giá trị của R4 thoả mãn điều kiện bài toán.
Câu 11:
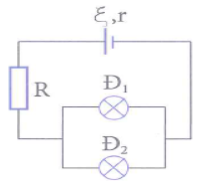
Cho mạch điện như hình vẽ:
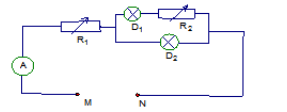
Đèn Đ1 loại 3 V - 1,5 W, đèn Đ2 loại 6 V - 3 W. Hiệu điện thế giữa hai điểm M và N là UMN = 9 V. Ampe kế A và dây nối có điện trở không đáng kể. Điều chỉnh cho R1 = 1,2 \[\Omega \] và R2 = 2 \[\Omega \]. Tìm số chỉ của ampe kế, các đèn sáng thế nào?
 Xem đáp án
Xem đáp án
Lời giải:
Mạch điện được mắc ![]()
Điện trở của bóng đèn Đ1 và Đ2 lần lượt là:
\[{R_{d1}} = \frac{{{U_{d1}}^2}}{{{P_{d1}}}} = \frac{{{3^2}}}{{1,5}} = 6\Omega \]
\[{R_{d2}} = \frac{{{U_{d2}}^2}}{{{P_{d2}}}} = \frac{{{6^2}}}{3} = 12\Omega \]
Khi điều chỉnh \[{R_1} = 1,2{\rm{ }}\Omega ;{\rm{ }}{R_2}\; = 2\,\Omega \] khi đó điện trở tương đương đoạn mạch là:
\[{R_{MN}} = {R_1} + \frac{{{R_{d2}}({R_2} + {R_{d1}})}}{{{R_{d1}} + {R_{d2}} + {R_2}}} = 6\Omega \]
Cường độ dòng điện mạch chính là: \[I{\rm{ }} = {\rm{ }}{I_A}\; = \frac{{{U_{MN}}}}{R}\; = 1,5A\]
=> Số chỉ ampe kế là 1,5A
Hiệu điện thế hai đầu bóng đèn là:
![]()
Suy ra lúc này bóng đèn sáng hơn lúc bình thường
Hiệu điện thế hai đầu bóng đèn là:
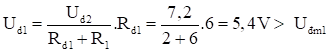
Suy ra bóng đèn Đ1 sáng hơn lúc bình thường.
Câu 12:
a. Hệ số Poát xông.
b. Độ tăng nội năng của khối khí đó.
c. Công mà khối khí đó thực hiện được.
 Xem đáp án
Xem đáp án
Lời giải:
a. Ta có: \(Q = \frac{m}{\mu }.{C_p}.\Delta T = {C_p}\Delta T\)
\({C_p} = \frac{Q}{{\Delta T}} = \frac{{i + 2}}{2}R \Rightarrow i = 3\)
\(\gamma = \frac{{i + 2}}{i} = 1,67\)
b. \(\Delta U = \frac{i}{2}.R.\Delta T = 0,72MJ\)
c. \(A = \Delta U - Q = - 0,48MJ\)( sinh công )
Câu 13:
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: 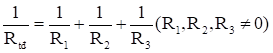
Mà 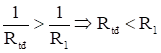
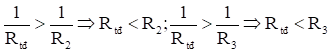
Câu 14:
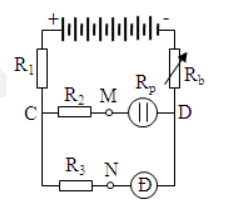
Cho mạch điện như hình vẽ. Trong đó bộ nguồn gồm 8 nguồn giống nhau, mỗi cái có suất điện động 5V, có điện trở trong \(0,25\,\,\Omega \) mắc nối tiếp, đèn Đ có loại 4V - 8W, \({R_1} = 3\Omega \), \({R_2} = {R_3} = 2\Omega \), \({R_p} = 4\Omega \) và \({R_p}\)là bình điện phân đựng dung dịch \(A{l_2}{(S{O_4})_3}\)có cực dương bằng Al. Đương lượng gam của nhôm là 9. Điều chỉnh biến trở \({R_b} = a(\Omega )\) thì đèn Đ sáng bình thường lúc này độ lớn hiệu điện thế giữa hai điểm M và N là b (V). Khối lượng Al giải phóng ở cực âm trong thời gian (a + b) giờ là:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án D
\({E_p} = 8.5 = 40V;\,\,{r_p} = 8.0,25 = 2\Omega \)
Ta có: \({R_D} = \frac{{{4^2}}}{8} = 2\,\,\Omega ;\,\,{I_D} = {I_{dm}} = \frac{4}{2} = 2A\) (do đèn sáng bình thường)
\({R_{3D}} = 2 + 2 = 4\Omega ;{R_{2p}} = 2 + 4 = 6\Omega \)
\({U_{CD}} = {U_{3D}} = {I_D}.{R_{3D}} = 2.4 = 8V\)
\({U_{CD}} = {U_{2p}} = {U_{3D}} = {I_p}.{R_{2p}} \Leftrightarrow {I_p}.6 = 8 \Rightarrow {I_p} = \frac{4}{3}A\)
\( \Rightarrow I = {I_p} + {I_D} = 2 + \frac{4}{3} = \frac{{10}}{3}A\)
Cường độ dòng điện mạch ngoài: \(I = \frac{{{E_b}}}{{{R_{td}} + {r_b}}} \Rightarrow \frac{{10}}{3} = \frac{{40}}{{{R_{td}} + 2}} \Rightarrow {R_{td}} = 10\Omega \)
\({R_{td}} = {R_1} + {R_b} + \frac{{{R_{2p}}.{R_{3D}}}}{{{R_{2p}} + {R_{3D}}}} \Rightarrow {R_b} = 4,6\Omega \Rightarrow a = 4,6\)
Ta có: \({U_{MN}} = {U_{MD}} - {U_{ND}} = {U_p} - {U_D} = {I_p}.{R_p} - {U_D} = \frac{4}{3}.4 - 4 = \frac{4}{3}V \Rightarrow b = \frac{4}{3}\)
Khối lượng Al giải phóng ở cực âm: \(m = \frac{1}{{96500}}.9.\frac{4}{3}.\left( {4,6 + \frac{4}{3}} \right).60.60 = 2,66g\)
Câu 15:
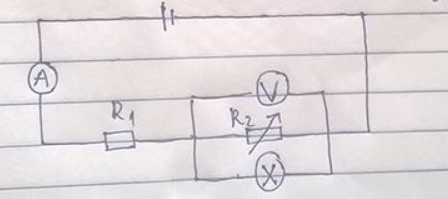
Cho mạch chứa nguồn có E = 12V, r = 1 \(\Omega \), đèn 6V - 3W, \({R_1} = 5\Omega \), \({R_2}\) là một biến trở. Biết \({R_v} = \infty \), \({R_A} = 0\).
a. Cho \({R_2} = 6\Omega \). Tìm số chỉ vôn kế, ampe kế. Hỏi đèn sáng như thế nào.
b. Tìm \({R_2}\)để đèn sáng bình thường.
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: ![]()
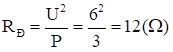
a. \({R_2} = 6\Omega \)
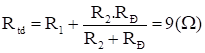
\( \to I = \frac{E}{{{R_{td}} + r}} = \frac{{12}}{{1 + 9}} = 1,2(A)\)
Có: ![]()
![]()
![]() \( \to {U_V} = 4,8(V)\)
\( \to {U_V} = 4,8(V)\)
\({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{{4,8}}{6} = 0,8(A)\)
Vậy đèn sáng yếu hơn bình thường.
b. Để đèn sáng bình thường thì \({I_d} = {I_{dm}} = \frac{3}{6} = 0,5A\)
\({U_d} = {U_{dm}} = 6V = {U_2} = {U_{CB}} = {U_{2d}};{U_{AC}} = {U_1}\)
Ta có:\({U_{AB}} = {U_{AC}} + {U_{CB}}\)\( \Leftrightarrow E - I.r = {U_1} + {U_{2d}}\)\( \Leftrightarrow E - I.r = {I_1}.{R_1} + 6\)\( \Leftrightarrow 12 - I = I.5 + 6\)
\( \to I = {I_1} + 1A\)
\({I_1} = {I_{2d}} = {I_2} + {I_d} \Rightarrow {I_2} = {I_1} - {I_d}\)\[ = 1 - 0,5 = 0,5A\]\[ \Rightarrow {R_2} = \frac{{{U_2}}}{{{I_2}}} = \frac{6}{{0,5}} = 12\Omega \]
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải:
Thời gian rơi của vật là: \[t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.180}}{{10}}} = 6(s)\]
Gọi vận tốc đầu của vật là \[{v_0}\].
Ta có: \[v = \sqrt {{v_0}^2 + {{(g.t)}^2}} = \sqrt {{v_0}^2 + {{(10.6)}^2}} = 100\]\[ \Rightarrow {v_0} = 80(m/s)\]
Tầm xa của vật: \[L = {v_0}.t = 80.6 = 480(m)\]
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải:
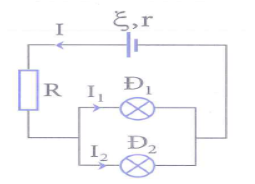
Mỗi bóng đèn dây tóc có bản chất là một điện trở có giá trị R. Nếu Uđm và Pđm lần lượt là điện áp định mức và công suất định mức của bóng đèn, khi đó ta có:
\[{P_{dm}} = \frac{{U_{dm}^2}}{R} \Rightarrow R = \frac{{U_{dm}^2}}{{{P_{dm}}}}\]
Cường độ dòng điện qua các bóng đèn là:
\[{R_{d1}} = \frac{{{{12}^2}}}{6} = 24\,\Omega ;\,{R_{d2}} = \frac{{{{12}^2}}}{{12}} = 12\,\Omega \]
\[{R_m} = R + {R_{d12}} = 3 + 8 = 11\,\Omega \]
\[{I_c} = \frac{E}{{{R_m} + r}} = \frac{{24}}{{11 + 1}} = 2\,A\]
\[{U_1} = {U_2} = {U_{12}} = I.{R_{d12}} = 2.8 = 16\,V\]
\[{I_1} = \frac{{{U_1}}}{{{R_{td}}}} = \frac{{16}}{{24}} = \frac{2}{3}A & ;\,\,{I_2} = \frac{{{U_2}}}{{{R_{d2}}}} = \frac{{16}}{{12}} = \frac{4}{3}A\]
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: \[x = {x_0} + {v_0}t + \frac{1}{2}.a.{t^2}\] và v = v0 + at
Giải hệ: \[\left\{ \begin{array}{l}3 = {x_0} + {v_0}4 + \frac{1}{2}.a{.4^2}\\8 = {x_0} + {v_0}5 + \frac{1}{2}.a{.5^2}\\6 = {v_0} + a.5\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 3\,m\\{v_0} = - 4\,m/s\\a = 2\,m/{s^2}\end{array} \right.\]
Gia tốc là: \[a = 2m/{s^2}\]
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
\[A = {W_{d2}} - {W_{d1}} \Leftrightarrow qU = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 \Leftrightarrow - {1,6.10^{ - 19}}.U = 0 - \frac{1}{2}{.9,1.10^{ - 31}}.{\left( {{{3.10}^7}} \right)^2}\]
\[ \Rightarrow U = 2559,375\,\left( V \right)\]
Mà \[U = {V_A} - {V_B} \Rightarrow 2559,375 = 6000 - {V_B} \Rightarrow {V_B} = 3440,6\,\left( V \right)\]
Câu 20:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
Vì A liên quan đến lí thuyết còn B, C, D là thực nghiệm.
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải:
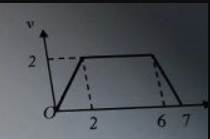
Từ 0 đến 2 s: chất điểm chuyển động thẳng nhanh dần đều với gia tốc:
\[{a_1} = \frac{{2 - 0}}{2} = 1\,m/{s^2}\]
Từ 2s đến 6s: chất điểm chuyển động thẳng đều với vận tốc v = 2 m/s; a = 0.
Từ 6s đến 7s: chất điểm chuyển động thẳng chậm dần đều với gia tốc:
\[{a_2} = \frac{{0 - 2}}{1} = - 2\,m/{s^2}\]
Câu 22:
 Xem đáp án
Xem đáp án
Lời giải:
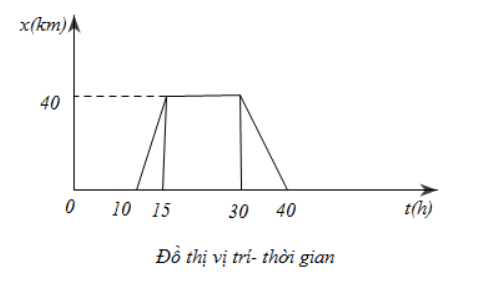
+Trong khoảng thời gian từ 0h đến 10h:
Tọa độ x = 0, vật đứng yên tại gốc toạ độ O
+ Trong khoảng thời gian từ 10h đến 15h
Vật chuyển động từ gốc O đến vị trí có x = 40 km, tức là theo chiều dương, với vận tốc trung bình: \[{v_{tb}} = \frac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}} = \frac{{40 - 0}}{{15 - 10}} = 8km/h\]
+ Trong khoảng thời gian từ 15h đến 30h: Toạ độ luôn là x = 40 km, vật đứng yên tại vị trí này.
+ Trong khoảng thời gian từ 30h đến 40h: Vật chuyển động từ vị trí có x = 40 km đến vị trí có x = 0 (theo chiều âm), với vận tốc trung bình là: \[{v_{tb}} = \frac{{0 - 40}}{{40 - 30}} = - 4km/h\]
+Từ 40h trở đi: Vật đứng yên tại gốc O. Ta có sơ đồ chuyển động:

Và nếu chỉ để ý sự biến thiên của vận tốc theo thời gian, ta vẽ được đồ thị vận tốc- thời gian:
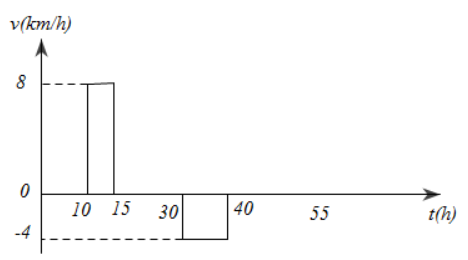
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án D
Tỉ số giữa thời gian lò xo nén và dãn trong một chu kì là \[\frac{1}{3}\] nên thời gian lò xo bị nén trong một chu kì là 0,25T, vị trí lò xo không biến dạng là:
\(x = \Delta \ell = A\frac{{\sqrt 2 }}{2} \to A = 10\sqrt 2 (cm)\)
\({v_{\max }} = \omega A = \sqrt {\frac{g}{{\Delta \ell }}} .A = 100\sqrt 2 (cm/s)\)Câu 24:
 Xem đáp án
Xem đáp án
Lời giải:
Lực điện tổng hợp bằng 0.
\[ \Rightarrow {\overrightarrow F _{13}} + {\overrightarrow F _{23}} = \overrightarrow 0 ;{\overrightarrow F _{13}} \uparrow \downarrow {\overrightarrow F _{23}}\]\[ \Rightarrow {F_{13}} = {F_{23}} \Rightarrow k \cdot \frac{{|{q_1}{q_3}|}}{{{r^2}_{13}}} = k \cdot \frac{{|{q_2}{q_3}|}}{{{r^2}_{23}}}\]
\[ \Rightarrow \frac{{\left| { - {{10}^{ - 8}} \cdot 2 \cdot {{10}^{ - 8}}} \right|}}{{r_{13}^2}} = \frac{{\left| {4 \cdot {{10}^{ - 8}} \cdot 2 \cdot {{10}^{ - 8}}} \right|}}{{r_{23}^2}} \Leftrightarrow \frac{1}{{{r^2}_{13}}} = \frac{4}{{{r^2}_{23}}} \Rightarrow \frac{{{r_{13}}}}{{{r_{23}}}} = \frac{1}{2}\,\,\,(1)\]
Do hai điện tích trái dấu nên để lực điện tổng hợp tác dụng lên điện tích q3 bằng không thì điện tích q3 phải nằm trên đường nối A và B nhưng ở ngoài khoảng AB.
Do độ lớn điện tích q1 nhỏ hơn độ lớn điện tích q2 nên q3 sẽ nằm gần q1 hơn:
\[{r_{23}} - {r_{13}} = 6\,\,(2)\]
Từ (1) và (2) \[ \Rightarrow \left\{ \begin{array}{l}{r_{13}} = 6\,cm\\{r_{23}} = 12\,cm\end{array} \right.\]
Đặt điện tích \[{q_3}\]ngoài khoảng AB và cách \[{q_1}\]một đoạn 6 cm và cách \[{q_2}\]một đoạn 12 cm.
Câu 25:
 Xem đáp án
Xem đáp án
Lời giải:
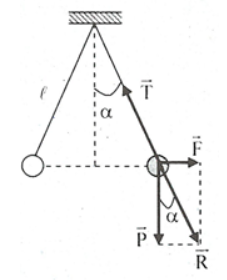
Các lực tác dụng lên mỗi quả cầu gồm: trọng lực \[\overrightarrow P \], lực tương tác tĩnh điện \[{\overrightarrow F _d}\] và lực căng của dây treo \[\overrightarrow T \].
Khi quả cầu cân bằng thì: \[\underbrace {\overrightarrow P + {{\overrightarrow F }_d}}_{\overrightarrow R } + \overrightarrow T = \overrightarrow 0 \Leftrightarrow \overrightarrow R + \overrightarrow T = \overrightarrow 0 \]
\[ \Rightarrow \overrightarrow R \] có phương sợi dây \[ \Rightarrow \tan \alpha = \frac{F}{P} \Rightarrow F = P.\tan \alpha = P\frac{{\frac{R}{2}}}{{\sqrt {{\ell ^2} - {{\left( {\frac{R}{2}} \right)}^2}} }}\]
Nhận thấy: \[{\ell ^2} > > {\left( {\frac{R}{2}} \right)^2} \Rightarrow {\ell ^2} - {\left( {\frac{R}{2}} \right)^2} \approx {\ell ^2} \Rightarrow \sqrt {{\ell ^2} - {{\left( {\frac{R}{2}} \right)}^2}} \approx \ell \Rightarrow F \approx \frac{{PR}}{{2\ell }}\]
Lúc đầu: \[{F_1} = k\frac{{{q^2}}}{{{R^2}}} = \frac{{PR}}{{2\ell }}\,\,\,\,\left( 1 \right)\]
Giả sử ta chạm tay vào quả cầu 1, kết quả sau đó quả cầu 1 sẽ mất điện tích, lúc đó giữa hai quả cầu không còn lực tương tác nên chính sẽ trở về vị trí dây thẳng đứng. Khi chúng vừa chạm nhau thì điện tích của quả 2 sẽ truyền sang cho quả 1 và lúc này điện tích mỗi quả sẽ là: \[{q_1}' = {q_2}' = \frac{{{q_2}}}{2} = \frac{q}{2} \Rightarrow {F_2} = k\frac{{{q^2}}}{{4{{\left( {R'} \right)}^2}}} = \frac{{PR'}}{{2\ell }}\,\,\,\left( 2 \right)\]
Từ (1) và (2) ta có: \[4{\left( {R'} \right)^3} = {R^3} \Rightarrow R' = \frac{R}{{\sqrt[3]{4}}} \approx 4\,cm\]
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án B
Câu 27:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án C
Động năng cực đại: \[{W_{d\max }} = \frac{1}{2}k{A^2} = \frac{1}{2}{.80.0,02^2} = 0,016\,J = 16mJ\]
Câu 28:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án B
Điện áp định mức của tụ 220 V và trị số điện dung của tụ điện là 1000pF.
Câu 29:
 Xem đáp án
Xem đáp án
Lời giải:
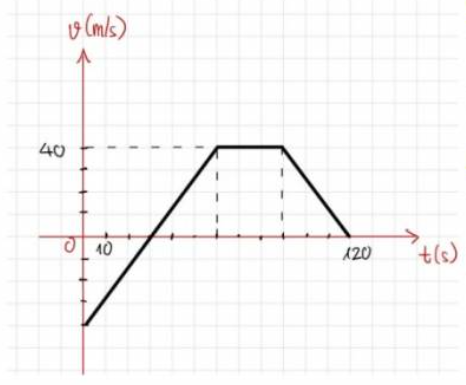
Giai đoạn từ A đến B là chuyển động nhanh dần đều.
Giai đoạn từ B đến C là chuyển động đều.
Giai đoạn từ C đến D là chuyển động chậm dần đều.
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải:
Sau 4 h từ khi thả hòn đá đến khi người đó nghe thấy tiếng hòn đá đập vào đáy giếng → 4 s chính là thời gian hòn đá rơi + thời gian âm thanh do hòn đá va chạm với đáy giếng tạo ra truyền đến tai người đó.
Thời gian hòn đá rơi: \({t_1} = \sqrt {\frac{{2h}}{g}} \)
Thời gian âm thanh truyền từ đáy giếng đến tai người: \({t_2} = \frac{h}{v} = \frac{h}{{340}}\)
\( \Rightarrow 4 = \frac{h}{{340}} + \sqrt {\frac{{2h}}{g}} \Rightarrow h \approx 71\,\,m\)
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải:
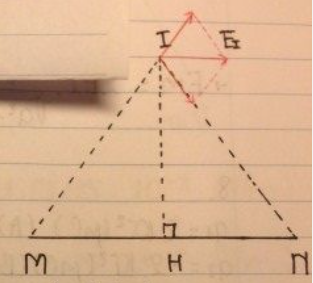
- Do \({\overrightarrow E _I}\) nằm trên đường trung trực MN →\(\left| {{q_1}} \right| = \left| {{q_2}} \right|\)
- Do \({\overrightarrow E _I}\) nằm // MN →\({q_1}\).\({q_2}\)< 0
Vậy \(\left[ \begin{array}{l}{q_1} > \;0,\,\,{q_2} < \;0,\,\,\left| {{q_1}} \right| = \left| {{q_2}} \right|\\{q_1} < \;0,\,\,{q_2} > 0,\,\,\left| {{q_1}} \right| = \left| {{q_2}} \right|\end{array} \right.\)
Câu 32:
Khi mắc 2 đầu dây dẫn kim loại vào một hiệu điện thế U = 15 V có các electron tự do chạy qua và tạo thành dòng điện không đổi, trong thời gian 10 s có điện lượng q = 9,6 C đi qua. Tìm:
a. Cường độ dòng điện qua dây dẫn.
b. Sơ electron đã đi qua tiết diện ngang dây dẫn trong 10 s.
 Xem đáp án
Xem đáp án
Lời giải:
a. Cường độ dòng điện qua dây dẫn là: \(I = \frac{q}{t} = \frac{{9,6}}{{10}} = 0,96A\)
b. Số electron đi qua tiết diện trong 10s: \(N = \frac{q}{{\left| e \right|}} = \frac{{9,6}}{{{{1,6.10}^{ - 19}}}} = {6.10^{19}}\)
Câu 33:
 Xem đáp án
Xem đáp án
Lời giải:
Do xe chuyển động chậm dần nên gia tốc a có giá trị âm.
Gọi vận tốc ban đầu là \[{v_0}\], vận tốc sau 5 s là \[{v_1}\], khi dừng lại vận tốc bằng 0, ta có:
\[0 = {v_0} + a.t \Rightarrow {v_0}\, = - a.t = - 10.a\]
\[{v_1}\, = {v_0} + a.t\prime = - 10.a + a.5 = - 5a\]
Áp dụng công thức độc lập:
\[v_1^2 - v_0^2 = 2aS\]\[ \Rightarrow {( - 5a)^2} - {( - 10a)^2} = 2aS \Rightarrow - 75a = 2.37,5 \Rightarrow a = - 1\,m/{s^2}\]
Câu 34:
 Xem đáp án
Xem đáp án
Lời giải:
Áp suất đáy ở mỗi nhánh bình thông nhau sẽ bằng nhau.
Khi chưa đặt quả cân lên, ta sẽ có:
\(\frac{{10{M_1}}}{{{S_1}}} + d.{h_1} = \frac{{10{M_2}}}{{{S_2}}} + d.{h_2}\)\( \Leftrightarrow \frac{{10{M_2}}}{{{S_2}}} - \frac{{10{M_1}}}{{{S_1}}} = d.({h_1} - {h_2}) = d.0,1\,\,(1)\)
Khi đặt quả cân 2 kg lên pittông 1: \(\frac{{10({M_1} + m)}}{{{S_1}}} = \frac{{10{M_2}}}{{{S_2}}}\)
Thay số tính được: \({S_2} = \frac{2}{3}{S_1}\)
Thay vào (1) được: \({S_1} = \frac{{200}}{{0,1.d}}\,\,(2)\)
Đặt quả cân 2 kg lên pittông thứ 2 ta sẽ có:
\(\frac{{10{M_1}}}{{{S_1}}} + d.{h_1}^' = \frac{{10({M_2} + m)}}{{{S_2}}} + d.{h_2}^'\)\( \Leftrightarrow \frac{{400}}{{{S_2}}} - \frac{{100}}{{{S_1}}} = d.\Delta H\)\( \Leftrightarrow \frac{{500}}{{{S_1}}} = d.\Delta H\)
\( \Rightarrow \Delta H = 25cm\)
Câu 35:
Hai bình hình trụ có tiết diện \[{s_1}\], \[{s_2}\] được thông với nhau bằng một ống nhỏ và có chứa nước. Trên mặt nước có đặt các pittông mỏng, khối lượng \[{m_1}\], \[{m_2}\]. Khi đặt một quả cân m = 1 kg trên pittông \[{s_1}\] thì mực nước bên pittông có quả cân thấp hơn mực nước bên kia một đoạn \[{h_1}\]= 20 cm. Khi đặt quả cân sang pittông \[{s_2}\] thì mực nước bên quả cân thấp hơn bên này một đoạn \[{h_2}\] = 5 cm. Biết \[{s_1}\] = 1,5\[{s_2}\], \[{m_1}\] = \[{m_2}\]
a. Tìm khối lượng các pittông.
b. Tìm độ chênh lệch mực nước ở hai bình khi chưa đặt quả cân, cho khối lượng riêng của nước là D = 1000 kg/m3.
 Xem đáp án
Xem đáp án
Lời giải:
Áp suất tại điểm A: \({p_A} = {p_0} + \frac{{10m}}{{{S_1}}} + \frac{{10{m_1}}}{{{S_1}}}\)
Áp suất tại điểm B: \({p_B} = {p_0} + 10.D.h + \frac{{10{m_2}}}{{{S_2}}}\)
Áp dụng tính chất bình thông nhau: \({p_A} = {p_B}\)
\({p_0} + \frac{{10m}}{{{S_1}}} + \frac{{10{m_1}}}{{{S_1}}} = {p_0} + 10.D.h + \frac{{10{m_2}}}{{{S_2}}}\)\( \Leftrightarrow \frac{{10m}}{{{S_1}}} + \frac{{10{m_1}}}{{{S_1}}} = 10.D.{h_1} + \frac{{10{m_2}}}{{{S_2}}}(1)\)
\({p_A}^' = {p_0} + \frac{{10{m_1}}}{{{S_1}}} + 10.D.{h_2}\)
\({p_B}^' = {p_0} + \frac{{10{m_2}}}{{{S_2}}} + \frac{{10m}}{{{S_2}}}\)
\( \to {p_A}^' = {p_B}^'\)\( \to \frac{{10{m_1}}}{{{S_1}}} + 10.D.{h_2} = \frac{{10{m_2}}}{{{S_2}}} + \frac{{10m}}{{{S_2}}}\,\,(2)\)
Trừ vế theo vế của phương trình (1) cho phương trình (2):
\(\frac{{10m}}{{{S_1}}} - 10.D.{h_2} = 10.D.{h_1} - \frac{{10m}}{{{S_2}}}\)\( \Leftrightarrow \frac{{10m}}{{{S_1}}} + \frac{{10m}}{{{S_2}}} = 10.D.({h_1} + {h_2})\)
\( \Leftrightarrow \frac{{50m}}{{3{S_1}}} = 10.D.({h_1} + {h_2})\,\,(v\`i \,\,{S_1} = 1,5{S_2})\)
\( \Leftrightarrow {S_1} = \frac{{50m}}{{1000.3.10.({h_1} + {h_2})}} = \frac{{50.1}}{{1000.3.10.(20 + 5){{.10}^{ - 2}}}} = \frac{1}{{150}}{m^2}\)\( \Rightarrow {S_2} = \frac{1}{{100}}{m^2}\)
Thay vào phương trình (1):
\(\frac{{10.1}}{{\frac{1}{{150}}}} + \frac{{10.{m_1}}}{{\frac{1}{{150}}}} = 10.1000.0,2 + \frac{{10.{m_2}}}{{\frac{1}{{100}}}}\) \( \Leftrightarrow 1500 + 1500{m_1} = 2000 + 1000{m_1}({m_2} = {m_1})\)
\( \Leftrightarrow 500{m_1} = 500\)\( \Leftrightarrow {m_1} = 1(kg)\)\( \to {m_2} = 1(kg)\)
b. Khi chưa có quả cân: sát tại mặt thoáng:
\({p_C} = {p_0} + \frac{{10{m_1}}}{{{S_1}}} = {p_0} + \frac{{10.1}}{{\frac{1}{{150}}}} = {p_0} + 1500\)
\({p_D} = {p_0} + \frac{{10{m_2}}}{{{S_2}}} = {p_0} + \frac{{10.1}}{{\frac{1}{{100}}}} = {p_0} + 1000\)
\( \to {p_C} > \;{p_D}\)\( \to {p_C} = {p_0} + 10.D.h\)
\( \Leftrightarrow {p_0} + 1500 = {p_0} + 1000 + 10.1000.h\)\( \Leftrightarrow 500 = 10000.h\)\( \Leftrightarrow h = 0,05(m)\)
Câu 36:
 Xem đáp án
Xem đáp án
Lời giải:
Quãng đường người đi xe đạp đi được: \[{s_1} = 2.10 = 20\,\,km\]
Quãng đường người đi xe máy đi được: \[{s_2} = 1.30 = 30\,\,km\]
Quãng đường người đi xe máy cách người đi xe đạp: \[s = {s_2} - {s_1} = 30 - 20 = 10\,\,km\]
Từ lúc ô tô xuất phát, xe đạp đã ở giữa xe máy và ô tô, nên lần đầu tiên 3 xe cách đều nhau có thứ tự là: ô tô - xe đạp - xe máy.
Thời điểm lúc 3 xe cách đều nhau:
\[{s_1} - t({v_3} - {v_1}) = t({v_2} - {v_{1}}) + s\]\[ \Leftrightarrow 20 - 30t = 20t + 10\]\[ \Rightarrow t = \frac{1}{5}h = 12\,\]phút.
Vậy vào lúc 9h12 phút thì 3 xe cách đều nhau lần đầu tiên theo thứ tự: oto – xe đạp – xe máy.
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án C
\({F_{\max }} = kA = m{\omega ^2}A = m\frac{{4{\pi ^2}}}{{{T^2}}}A = 0,4.\frac{{4{\pi ^2}}}{{{{0,5}^2}}}.0,08 = 5,05N\)
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án C
\[T = 0,5s = > \omega = 4\pi \;rad/s\]
\[\omega = \sqrt {\frac{k}{m}} = > k = {\omega ^2}.m = {(4\pi )^2}.0,1 = 15,79\;N/m\]z
\[ = > {F_{max}} = \left| {k.A} \right| = \left| {15,79.0,08} \right| = 1,26\;N\]
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải:
a. Áp dụng công thức: \(I = \frac{q}{t} \Rightarrow q = It\)
Thay số: \(q = 0,5 \times 10 \times 60 = 60C\)
b. Số êlectron dịch chuyển qua tiết diện thẳng của dây tóc:
\(N = \frac{q}{{\left| e \right|}} = \frac{{60}}{{{{1,6.10}^{ - 19}}}} = {3,75.10^{20}}\)
Câu 40:
 Xem đáp án
Xem đáp án
Lời giải:
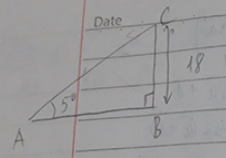
Xét ∆ABC vuông tại B có góc A = 5°
=> \[AC = \frac{{18}}{{\sin {5^0}}} = 206,5\,m\]
18 km/h = 5 m/s
Thời gian người đó đi mất là: \(t = \frac{{206,5}}{5} = 41,3\,(s)\)
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải:
Độ dài dốc là: \[\frac{{15}}{{sin{4^0}}} = 215(m) = 0,215(km)\]
Vậy thời gian người đó lên tới đỉnh dốc là:
\[\frac{{0,215}}{9} = \frac{{43}}{{1800}}(h) = 1\,\,ph\'u t\,\,26\,\,gi\^a y\]
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án D
Năng lượng của con lắc lò xo: \[W = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2}\]
Câu 43:
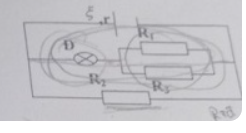
Cho \(E = 12(V),r = 3\,\Omega ,{R_1} = 4\,\Omega ,{R_2} = 6\,\Omega ,{R_3} = 4\,\Omega \). Đèn ghi (4 V – 4 W)
a. Tính Rtđ ?
b. I, U qua mỗi điện trở? Và độ sáng của đèn?
c. Thay \({R_2}\)bằng một tụ điện có điện dung \(C = 20\mu F\). Tính điện tích của tụ?
 Xem đáp án
Xem đáp án
Lời giải:
a) Điện trở của đèn: \[{R_D} = \frac{{U_D^2}}{{{P_D}}} = \frac{{{4^2}}}{4} = 4\,\Omega \]
\[{R_{D13}} = {R_D} + {R_{13}} = {R_D} + \frac{{{R_1}{R_3}}}{{{R_1} + {R_3}}} = 4 + \frac{{4.4}}{{4 + 4}} = 6\,\Omega \]
\[{R_{td}} = \frac{{{R_{D13}}.{R_2}}}{{{R_{D13}} + {R_2}}} = \frac{{6.6}}{{6 + 6}} = 3\,\Omega \]
b) Cường độ qua mạch chính: \[I = \frac{E}{{{R_{td}} + r}} = \frac{{12}}{{3 + 3}} = 2\,A\]
\[{U_{D13}} = {U_2} = U = I.{R_{td}} = 2.3 = 6V\]
\[{I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{6}{6} = 1\,A\]
\[{I_D} = {I_{13}} = {I_{D13}} = \frac{{{U_{D13}}}}{{{R_{D13}}}} = \frac{6}{6} = 1\,A\]
\[{U_{13}} = {I_{13}}.{R_{13}} = {I_{13}}.\frac{{{R_1}{R_3}}}{{{R_1} + {R_3}}} = 1.\frac{{4.4}}{{4 + 4}} = 2\,V = {U_1} = {U_3}\]
\[{I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{2}{4} = 0,5\,A;\,{I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{2}{4} = 0,5\,A\]
c) Thay \({R_2}\)bằng một tụ điện có điện dung \(C = 20\mu F\).
\[Q = C{U_2} = {20.10^{ - 6}}.6 = {1,2.10^{ - 4}}\,C\]
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
108 km/h = 30 m/s
18 km/h = 5 m/s
Xe chuyển động theo phương ngang, xe hãm phanh, nên công của trọng lực bằng 0, công của phản lực bằng 0, công của lực hãm bằng độ biến thiên động năng:
\[A = {W_{d2}} - {W_{d1}} = \frac{1}{2}m\left( {v_2^2 - v_1^2} \right) = - 136,5\,J\]
Câu 45:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án B
Nhiệt lượng cần cung cấp cho ấm nước sôi là Q
Nếu chỉ dùng điện trở R1 thì nhiệt lượng do bếp tỏa ra là: \[{Q_1} = I_1^2{R_1}{t_1} = \frac{{{U^2}}}{{{R_1}}}{t_1}\]
Nếu chỉ dùng điện trở R2 thì nhiệt lượng do bếp tỏa ra là: \[{Q_2} = I_2^2{R_2}{t_2} = \frac{{{U^2}}}{{{R_2}}}{t_2}\]
Bỏ qua sự mất nhiệt thì nhiệt lượng do bếp tỏa ra đều được cung cấp cho việc đun sôi nước ⇒ Q = Q1 = Q2.
\[ \Rightarrow \frac{{{U^2}}}{{{R_1}}}{t_1} = \frac{{{U^2}}}{{{R_2}}}{t_2} \Rightarrow \frac{{{t_1}}}{{{R_1}}} = \frac{{{t_2}}}{{{R_2}}} \Rightarrow \frac{{10}}{{10}} = \frac{{{t_2}}}{{20}} \Rightarrow {t_2} = 20\] (phút)Câu 46:
 Xem đáp án
Xem đáp án
Lời giải:
Đáp án A
+ Điện trở và cường độ dòng điện định mức của đèn
\[{R_d} = \frac{{{U^2}_d}}{{{P_d}}} = \frac{{{6^2}}}{3} = 12\Omega \]
\[{I_d} = \frac{{{P_d}}}{{{U_d}}} = \frac{3}{6} = 0,5A\]
\[ \to \] Cường độ dòng điện qua \[{I_2}\]là: \[{I_2} = \frac{{{U_d}}}{{{R_2}}} = \frac{6}{{12}} = 0,5A \to {I_m} = {I_2} + {I_d} = 1A\]
+ Cường độ dòng điện qua mạch là: \[{I_m} = \frac{E}{{{R_N} + r}}\]\[ \leftrightarrow 1 = \frac{{12}}{{5 + \frac{{12.12}}{{12 + 12}} + r}} \to r = 1\,\,\Omega \]
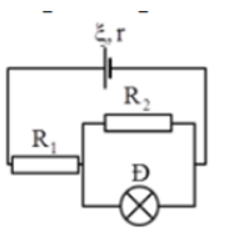
Câu 47:
Cho mạch điện có sơ đồ như hình vẽ trong đó các pin có suất điện động E1 = E2 = E3 = 3 V và có điện trở trong r1 = r2 = r3 = 1 \[\Omega \] các điện trở mạch ngoài R1 = R2 = R3 = 5 \[\Omega \]; R4 = 10 \[\Omega \].
a. Tính suất điện động và điện trở trong của bộ nguồn.
b. Tính hiệu điện thế hai đầu mỗi điện trở, tính hiệu điện thế UPQ.
c. Thay R4 bằng một tụ điện có điện dung \[25\,\mu F\] tính điện tích của tụ.
 Xem đáp án
Xem đáp án
Lời giải:
a. Các nguồn mắc nối tiếp, suất điện động bộ ngu: \[{E_b} = 3{E_1} = 9\,V\]
Điện trở trong bộ nguồn: \[{r_b} = 3{r_1} = 3\,\Omega \]
b. Điện trở mạch ngoài: \[{R_{td}} = \frac{{{R_{12}}.{R_{34}}}}{{{R_{12}} + {R_{34}}}} = \frac{{({R_1} + {R_2}).({R_3} + {R_4})}}{{{R_1} + {R_2} + {R_3} + {R_4}}} = 6\,\Omega \]
Cường độ dòng điện mạch chính: \[I = \frac{E}{{{R_{td}} + r}} = \frac{9}{{6 + 3}} = 1\,A\]
\[{U_{12}} = {U_{34}} = U = I.{R_{td}} = 1.6 = 6\,V\]
\[{I_{12}} = \frac{{{U_{12}}}}{{{R_{12}}}} = \frac{6}{{10}} = 0,6\,A = {I_1} = {I_2} \Rightarrow {U_1} = {I_1}{R_1} = 3\,V;\,{U_2} = {I_2}{R_2} = 3\,V\]
\[{I_{34}} = \frac{{{U_{34}}}}{{{R_{34}}}} = \frac{6}{{15}} = 0,4\,A = {I_3} = {I_4} \Rightarrow {U_3} = {I_3}{R_3} = 2\,V;\,{U_4} = {I_4}{R_4} = 4\,V\]
\[{U_{PQ}} = {U_3} - {U_1} = 2 - 3 = - 1\,V\] < 0
c. Thay R4 bằng một tụ điện có điện dung \[25\,\mu F\].
\[Q = C{U_4} = {25.10^{ - 6}}.4 = {10^{ - 4}}\,C\]Câu 48:
Một điện tích điểm \(q = {10^{ - 6}}\,C\) đặt trong không khí.
a) Xác định cường độ điện trường tại điểm cách điện tích 30 cm.
b) Đặt điện tích trong chất lỏng có hằng số điện môi là 16. Điểm có cường độ điện trường như câu a cách điện tích bao nhiêu?
 Xem đáp án
Xem đáp án
Lời giải:
a. Áp dụng công thức: \(E = \frac{{k\left| Q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}{{.10}^{ - 6}}}}{{{{0,3}^2}}} = {10^5}(V/m)\)
b. \(\varepsilon = 16 \Rightarrow E = \frac{{k\left| Q \right|}}{{\varepsilon r{'^2}}} \Rightarrow r' = \sqrt {\frac{{k\left| Q \right|}}{{E.\varepsilon }}} = 0,075\,m = 7,5\,cm\).
Câu 49:
 Xem đáp án
Xem đáp án
Lời giải:
Nhiệt kế là dụng cụ dùng để đo nhiệt độ. Nguyên tắc hoạt động của nhiệt kế dựa vào sự giãn nở vì nhiệt của chất lỏng trong nhiệt kế, và độ cao của chất lỏng trong nhiệt kế thay đổi phụ thuộc vào chất lỏng nở vì nhiệt nhiều hay ít (bầu nhiệt kế). Một số loại nhiệt kế thường gặp là: nhiệt kế rượu (đo nhiệt độ môi trường xung quanh), nhiệt kế y tế đo thân nhiệt của con người),... Ngoài ra còn có một số loại nhiệt kế hiện đại như nhiệt kế hồng ngoại, sử dụng cảm biến hồng ngoại để xác định nhiệt độ.
Câu 50:
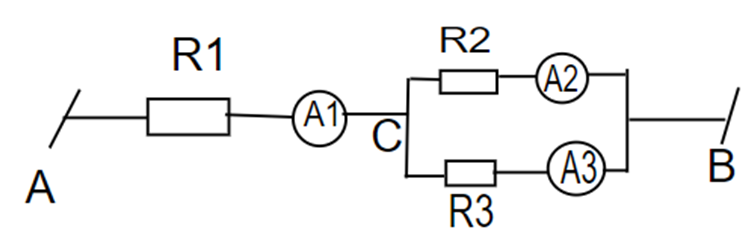
Cho mạch điện như hình vẽ. Biết R1 = 10 Ω, R2 = 3R3. Ampe kế A1 chỉ 4 A.
a. Tìm số chỉ của các ampe kế A2 và A3
b. Hiệu điện thế hai đầu điện trở R3 là 15 V. Tính hiệu điện thế giữa hai đầu đoạn mạch.
 Xem đáp án
Xem đáp án
Lời giải:
a. Ta có mạch điện: \[{R_1}nt({R_2}//{R_3})\]
Hiệu điện thế giữa 2 đầu điện trở \[{R_1}\]là: \[{U_1} = {I_1}.{R_1} = 4.10 = 40(V)\]
\[V\`i {\rm{ }}{R_1}{\rm{ }}nt{\rm{ }}\left( {{R_2}//{R_3}} \right) \Rightarrow {I_{1\;}} = {I_{23}}\; = I = 4\,A\]
\[{R_{23}} = \frac{{{R_2}.{R_3}}}{{{R_2} + {R_3}}} = \frac{{3{R_3}.{R_3}}}{{3{R_3} + {R_3}}} = \frac{{3{R_3}^2}}{{4{R_3}}} = 0,75{R_3}\]
\[ = > {\rm{ }}{U_{23}} = {U_2} = {U_3} = {I_{23}}.{R_{23}} = 4.0,75{R_3} = 3{R_3}\]
\[ \Rightarrow \left\{ \begin{array}{l}{I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{{3{R_3}}}{{3{R_3}}} = 1(A)\\{I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{{3{R_3}}}{{{R_3}}} = 3(A)\end{array} \right.\]
b. Ta có: \[{U_3} = 15V\]\[ \Rightarrow {U_2} = {U_3} = {U_{23}} = 15V\]
\[{R_1}{\rm{ }}nt{\rm{ }}\left( {{R_2}//{R_3}} \right){\rm{ }}n\^e n:\] hiệu điện thế giữa 2 đầu đoạn mạch là:
\[U = {U_1} + {U_{23}} = 40 + 15 = 55V\]
Câu 51:
Khi ô tô đang chạy với vận tốc 15 m/s trên một đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy chậm dần đều. Sau khi chạy thêm 125 m thì vận tốc của ô tô chỉ còn 10 m/s. Hãy tính :
a) Gia tốc của ô tô.
b) Thời gian ô tô chạy thêm được 125 m kể từ khi bắt đầu hãm phanh.
c) Thời gian chuyển động cho đến khi xe dừng hẳn.
 Xem đáp án
Xem đáp án
Lời giải:
a. Áp dụng công thức: \({v^2} - {v_0}^2 = 2as\)\( \Leftrightarrow {10^2} - {15^2} = 2a.125\)\( \Leftrightarrow a = - 0,5m/{s^2}\)
b. Phương trình vận tốc của ôtô: \(v = {v_0} + at = 15 - 0,5t\)
Sau khi chạy 125 m thì vận tốc oto còn 10 m/s.
\( \Rightarrow 10 = 15 - 0,5t\)\( \Leftrightarrow t = 10s\)
c. Khi xe dừng hẳn: \( \Rightarrow v = 0 \Rightarrow 0 = 15 - 0,5t \Rightarrow t = 30s\)
Câu 52:
Ô tô có khối lượng 1200 kg khi chạy trên đường nằm ngang với vận tốc v = 72 km/h thì tiêu hao 80 g xăng trên đoạn đường S = 1 km. Hiệu suất động cơ là 20%.
Tính công suất của ô tô. Cho biết khi 1 kg xăng bị đốt cháy thì tỏa ra năng lượng là 45.106 J.
 Xem đáp án
Xem đáp án
Lời giải:
72 km/h = 20 m/s
1 kg xăng bị đốt cháy thì tỏa ra năng lượng là 45.106 J.
Khi tiêu hao 80 g xăng trên đoạn đường S = 1 km thì năng lượng có ích là:
\[{A_{ci}} = \frac{{{{45.10}^6}}}{{1000}}.80 = {3,6.10^6}\,J\]
Năng lượng toàn phần: \[{A_{tp}} = \frac{{{A_{ci}}}}{H} = \frac{{{{3.10}^6}}}{{20\% }} = {18.10^6}\,J\]
Lực động cơ: \[{A_{tp}} = F.s \Rightarrow F = \frac{{{A_{tp}}}}{s} = \frac{{{{18.10}^6}}}{{1000}} = {18.10^3}\,N\]
Công suất động cơ: \[P = F.v = {18.10^3}.20 = {36.10^4}\,W\]Câu 53:
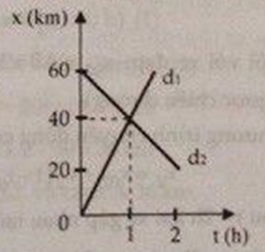
Đồ thị chuyển động của hai xe được biểu diễn như hình vẽ.
a) Lập phương trình chuyển động của mỗi xe.
b) Dựa trên đồ thị xác định vị trí và khoảng cách giữa hai xe sau thời gian 1,5 giờ kể từ khi xuất phát.
 Xem đáp án
Xem đáp án
Lời giải:
a. Phương trình chuyển động của hai xe
Xe 1 (ứng với đường d1): x1 = 40t
Xe 2 (ứng với đường d2): x2 = 60 - 20t
b. Sau thời gian 1,5 giờ thì vị trí của hai xe là:
x1 = 40t = 40.1,5 = 60 km
x2 = 60 - 20t = 60 – 20.1,5 = 30 km.
Khoảng cách của hai xe là 30 km.
