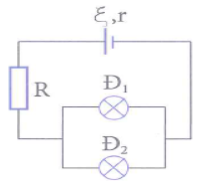
Đồ thị chuyển động của hai xe được biểu diễn như hình vẽ.
a) Lập phương trình chuyển động của mỗi xe.
b) Dựa trên đồ thị xác định vị trí và khoảng cách giữa hai xe sau thời gian 1,5 giờ kể từ khi xuất phát.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
a. Phương trình chuyển động của hai xe
Xe 1 (ứng với đường d1): x1 = 40t
Xe 2 (ứng với đường d2): x2 = 60 - 20t
b. Sau thời gian 1,5 giờ thì vị trí của hai xe là:
x1 = 40t = 40.1,5 = 60 km
x2 = 60 - 20t = 60 – 20.1,5 = 30 km.
Khoảng cách của hai xe là 30 km.
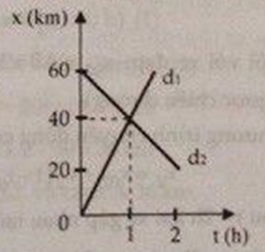
Cho mạch điện như hình vẽ:
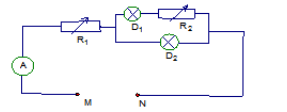
Đèn Đ1 loại 3 V - 1,5 W, đèn Đ2 loại 6 V - 3 W. Hiệu điện thế giữa hai điểm M và N là UMN = 9 V. Ampe kế A và dây nối có điện trở không đáng kể. Điều chỉnh cho R1 = 1,2 \[\Omega \] và R2 = 2 \[\Omega \]. Tìm số chỉ của ampe kế, các đèn sáng thế nào?
Ô tô có khối lượng 1200 kg khi chạy trên đường nằm ngang với vận tốc v = 72 km/h thì tiêu hao 80 g xăng trên đoạn đường S = 1 km. Hiệu suất động cơ là 20%.
Tính công suất của ô tô. Cho biết khi 1 kg xăng bị đốt cháy thì tỏa ra năng lượng là 45.106 J.
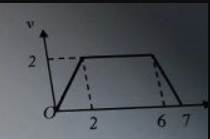
Khi ô tô đang chạy với vận tốc 15 m/s trên một đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy chậm dần đều. Sau khi chạy thêm 125 m thì vận tốc của ô tô chỉ còn 10 m/s. Hãy tính :
a) Gia tốc của ô tô.
b) Thời gian ô tô chạy thêm được 125 m kể từ khi bắt đầu hãm phanh.
c) Thời gian chuyển động cho đến khi xe dừng hẳn.
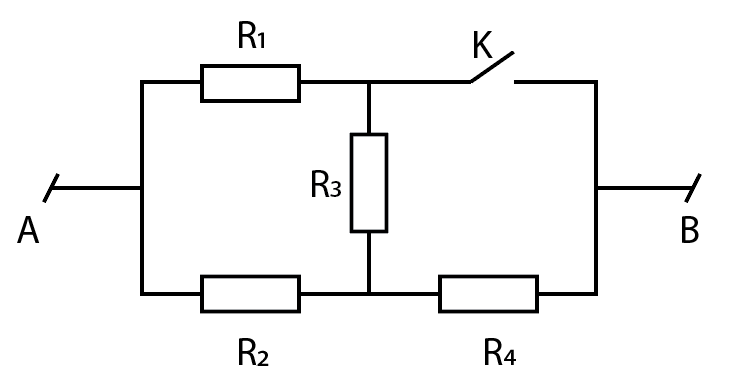
Cho mạch \[{R_1}nt\left( {\left( {{R_2}nt{R_3}} \right)//{R_4}} \right)\].
Biết \[{R_1} = 5\,\Omega ,{\rm{ }}{R_2} = 30\,\Omega ,{\rm{ }}{R_3} = {R_4} = 10\,\Omega \], r =2 \[\Omega \], E = 15 V.
a) Tìm nhiệt lượng toả ra trên \[{R_3}\] sau 3 phút 20 s.
b) Tìm UMN (M trước \[{R_1}\], N giữa \[{R_2}\] và \[{R_3}\]).