Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
\(y' = 4{x^3} + 3m{x^2} - 4x - 3m = \left( {x - 1} \right)\left[ {4{x^2} + \left( {4 + 3m} \right)x + 3m} \right]\)
\(y' = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{4{x^2} + \left( {4 + 3m} \right)x + 3m = 0\left( 2 \right)}\end{array}} \right.\)
Hàm số có 2 cực tiểu ⟺ y có 3 cực trị \( \Leftrightarrow y' = 0\) có 3 nghiệm phân biệt
⟺ (2) có 2 nghiệm phân biệt khác 1 \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\Delta = {{\left( {3m - 4} \right)}^2} > 0}\\{4 + 4 + 3m + 3m \ne 0}\end{array}} \right. \Leftrightarrow m \ne \pm \frac{4}{3}\)
Giả sử: Với \(m \ne \pm \frac{4}{3} \Rightarrow y' = 0\) có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\)
Từ bảng biến thiên ta thấy hàm số có 2 cực tiểu
Vậy hàm số có 2 cực tiểu khi \(m \ne \pm \frac{4}{3}\).
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{\frac{{{x_1} + {x_2}}}{2} = - 2}\\{\frac{{{y_1} + {y_2}}}{2} = - \frac{{2\left( {{x_1} + {x_2}} \right) + 10}}{2} = 9}\end{array}} \right.\).
Tọa độ trung điểm cực đại và cực tiểu là (–2; 9) không thuộc đường thẳng \(y = \frac{1}{2}x \Rightarrow m = - 3\) (không thỏa mãn)
Vậy m = 1 thỏa mãn điều kiện đề bài.
Một hồ bơi dạng hình hộp chữ nhật có kích thước trong lòng hồ là: Chiều dài 12m, chiều rộng 5m, chiều sâu 3m.
a. Tính thể tích của hồ bơi.
b. Tính diện tích cần lát gạch bên trong lòng hồ (mặt đáy và 4 mặt xung quanh).
c. Biết gạch hình vuông dùng để lát hồ bơi có cạnh 50cm. Hỏi cần mua ít nhất bao nhiêu viên gạch để lát bên trong hồ bơi.
Cho tứ giác ABCD có góc \(\widehat B = \widehat D = 90^\circ \).
a. Chứng minh rằng 4 điểm A, B, C, D cùng thuộc một đường tròn, tìm tâm đường tròn đó.
b. So sánh độ dài AC và BD. Tứ giác ABCD cần thêm điều kiện gì thì AC = BD?
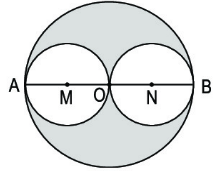
Cho hình tròn tâm O, đường kính AB = 8 cm.
a. Tính chu vi hình tròn tâm O đường kính AB, hình tròn tâm M, đường kính AO và hình tròn tâm N, đường kính OB.
b. So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
c. Tính diện tích phần đã tô đậm của hình tròn tâm O.