Giải bởi Vietjack
Lời giải
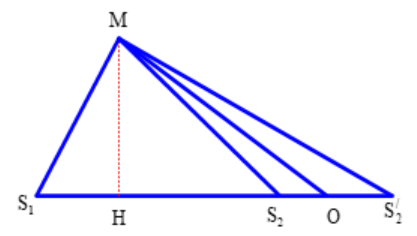
Xét \(\Delta M{S_1}{S_2}\)có \(M{S_1} = 16\left( {cm} \right);M{S_2} = 25\left( {cm} \right)\)
Ta có: \({S_1}{S_2} = {S_1}H + {S_2}H = \sqrt {{{16}^2} - M{H^2}} + \sqrt {{{25}^2} - M{H^2}} = 20\)
\( \Rightarrow MH = 15,98\left( {cm} \right) \Rightarrow M{S'_2} = 33,3\,cm\)
Gọi O là điểm nằm trong khoảng S2S'2 để đặt vị trí nguồn S2.
Tại M có cực đại giao thoa: \(MO - M{S_1} = k\lambda \)
Vì O nằm trên khoảng \({S_2}{S'_2} \Rightarrow M{S_2} - M{S_1} < k\lambda < M{S'_2} - M{S_1}\)
\( \Rightarrow 25 - 16 < 3k < 33,3 - 16 \Rightarrow 3 < k < 5,7 \Rightarrow k = 4;\,5\)
Có hai giá trị k thoả mãn.
Đáp án đúng: B
