Giải bởi Vietjack
Lời giải
Tại thời điểm ban đầu vật xuất phát từ VTCB đi theo chiều dương.
Chu kì dao động \(T = \frac{{2\pi }}{\omega } = 1\left( s \right)\)
Xét khoảng thời gian \(t = 12,375 = 12T + \frac{{3T}}{8}\)
Như vậy quãng đường đi được sẽ là s = s1 + s2
với s1 là quãng đường vật đi được trong thời gian 12T kể từ khi bắt đầu dao động, s2 là quãng đường vật đi được trong thời gian \(\frac{{3T}}{8}\) tiếp theo.
- Trong thời gian 12T, quãng đường vật đi được là s1 = 12.4A = 48A
- Trong thời gian \(\frac{{3T}}{8}\) tiếp theo, vật đi được quãng đường:
\({s_2} = A + \left( {A - \frac{{A\sqrt 2 }}{2}} \right) = 2A - \frac{{A\sqrt 2 }}{2}\)
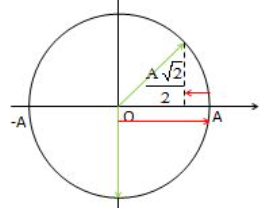
Vậy, tổng quãng đường đi được là: \(s = {s_1} + {s_2} = 48A + 2A - \frac{{A\sqrt 2 }}{2} = 50A - \frac{{A\sqrt 2 }}{2}\)
Thay số vào ta được s = 246,46 cm.
Đáp án đúng: B
