Giải bởi Vietjack
Lời giải
* Tần số góc của CLLX: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,1}}} = 10\sqrt 2 \left( {{\rm{rad/s}}} \right)\)
* Kéo quả cầu thẳng đứng xuống dưới vị trí cân bằng một đoạn \(2\sqrt 2 \) cm rồi thả cho quả cầu trở về vị trí cân bằng với vận tốc có độ lớn là \(0,2\sqrt 2 \left( {{\rm{m/s}}} \right) = 20\sqrt 2 \left( {{\rm{cm/s}}} \right)\)
⇒ Biên độ \(A = \sqrt {{x^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = 4\left( {cm} \right)\)
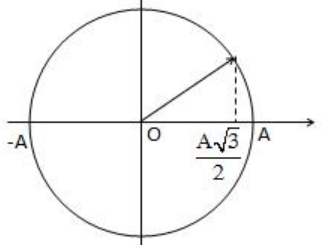
* Gốc thời gian là lúc thả quả cầu, nghĩa là lúc vật có li độ \(x = 2\sqrt 3 \) cm và chuyển động theo chiều âm(vì chiều dương hướng xuống)
=> Pha ban đầu φ = π/6 rad
Vậy, phương trình dao động của vật là:
\(x = 4\cos \left( {10\sqrt 2 t + \frac{\pi }{6}} \right)\left( {cm} \right) = 4\sin \left( {10\sqrt 2 t + \frac{{2\pi }}{3}} \right)\) cm.
Đáp án đúng: B
