Giải bởi Vietjack
Lời giải
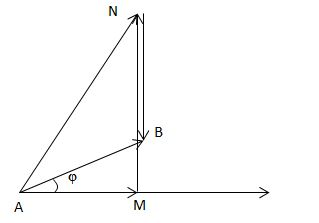
Ta vẽ được giản đồ véc tơ như sau:
Trong tam giác vuông MAB có: \(\widehat {MBA} + \varphi = {90^0} \Rightarrow \cos \varphi = \sin \widehat {MBA} = 0,8\)
Thấy rằng: \(\widehat {MBA} + \widehat {ABN} = {180^0} \Rightarrow \sin \widehat {ABN} = \sin \widehat {MBA} = 0,8\)
Do đó, \(\cos \widehat {ABN} = \pm \sqrt {1 - {{\sin }^2}\widehat {ABN}} = \pm 0,6\)
Vì \(\widehat {ABN}\) là góc tù nên cos\(\widehat {ABN}\)= -0,6
Trong tam giác ABN ta có: \(A{N^2} = A{B^2} + B{N^2} - 2AB.BN.\cos \widehat {ABN}\)
Tức là: \(U_{AN}^2 = U_{AB}^2 + U_{NB}^2 - 2{U_{AB}}.{U_{NB}}.\cos \widehat {ABN}\)
Thay số vào ta được: UAN = 400 V
Đáp án đúng: D
