Hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi M là trung điểm của OO’. Đường thẳng qua A cắt các đường tròn (O) và (O’) lần lượt ở C và D.
a) Khi CD ⊥ MA, chứng minh AC = AD.
b) Khi CD đi qua A và không vuông góc với MA.
i) Vẽ đường kính AE của (O), AE cắt (O’) ở H. Vẽ đường kính AF của (O’), AF cắt (O) ở G. Chứng minh AB, EG, FH đồng quy.
ii) Tìm vị trí của CD để đoạn CD có độ dài lớn nhất.
Giải bởi Vietjack
a)
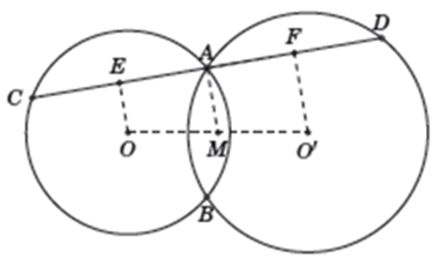
Gọi E, F theo thứ tự là trung điểm của AC, AD.
Suy ra OE ⊥ AC và AE = CE; O’F ⊥ AD và AF = DF.
Mà MA ⊥ CD (giả thiết).
Do đó OE // MA // O’F.
Khi đó tứ giác OO’FE là hình thang.
Hình thang OO’FE có MA // OE // O’F và M là trung điểm của OO’.
Suy ra MA là đường trung bình của hình thang OO’FE.
Do đó AE = AF.
Vì vậy 2AE = 2AF.
Vậy AC = AD (điều phải chứng minh).
b)
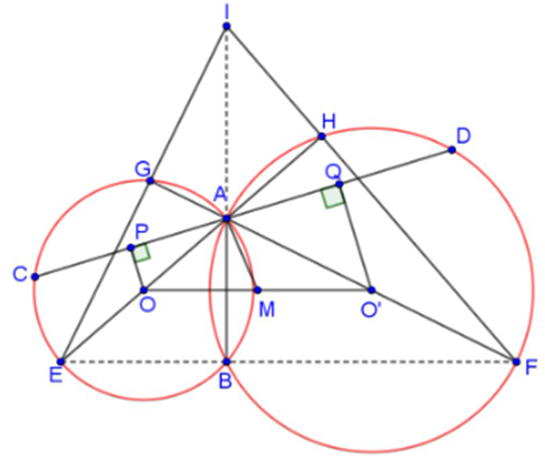
i) Gọi I là giao điểm của EG và FH.
Đường tròn (O) có AE là đường kính.
Suy ra AG ⊥ GE và AB ⊥ BE.
Đường tròn (O’) có AF là đường kính.
Suy ra AH ⊥ FH và AB ⊥ BF.
Ta có AB ⊥ BE (chứng minh trên) và AB ⊥ BF (chứng minh trên).
Suy ra ba điểm E, B, F thẳng hàng.
Do đó AB ⊥ EF.
Tam giác IEF có hai đường cao EH và FG cắt nhau tại A.
Suy ra A là trực tâm của tam giác IEF.
Mà AB ⊥ EF (chứng minh trên).
Do đó ba điểm I, A, B thẳng hàng.
Vậy AB, EG, FH đồng quy tại I.
ii) Kẻ OP ⊥ CD và O’Q ⊥ CD.
Suy ra P, Q lần lượt là trung điểm của AC, AD và OP // O’Q.
Khi đó AC = 2AP và AD = 2AQ.
Suy ra AC + AD = 2AP + 2AQ.
Vì vậy CD = 2PQ.
Do đó CD lớn nhất khi và chỉ khi PQ lớn nhất.
Ta có tứ giác OO’QP là hình thang vuông tại P, Q (vì OP // O’Q và OP ⊥ PQ).
Suy ra PQ ≤ OO’.
Dấu “=” xảy ra ⇔ OO’QP là hình chữ nhật.
⇔ PQ // OO’.
⇔ CD // OO’.
Vậy CD // OO’ thì CD có độ dài lớn nhất.
Có tất cả 40 con vừa gà vừa chó. Số chân chó nhiều hơn số chân gà là 16 chân. Hỏi có bao nhiêu gà, bao nhiêu chó?
Gọi S là tập hợp các giá trị của m để bất phương trình x2 – 2mx + 5m – 8 ≤ 0 có tập nghiệm là [a; b] sao cho b – a = 4. Tổng tất cả các phần tử của S là
Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn, biết rằng 3 lần số bi của bạn Hùng nhiều hơn 2 lần số bi của bạn Minh là 40 viên.
Cho tam giác ABC có các góc thỏa mãn \(\frac{{\sin A}}{1} = \frac{{\sin B}}{2} = \frac{{\sin C}}{{\sqrt 3 }}\). Tính số đo các góc của tam giác.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Cho tam giác ABC vuông cân tại A. Trên các cạnh góc vuông AB, AC lấy D và E sao cho AD = AE. Qua D vẽ đường thẳng vuông góc với BE cắt BC ở K. Qua A vẽ đường thẳng vuông góc với BE cắt BC ở H. Gọi M là giao điểm của DK và AC. Chứng minh rằng:
a) ∆BAE = ∆CAD;
b) ∆MDC cân;
c) HK = HC.
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.
a) Tứ giác MNPQ là hình gì? Vì sao?
b) Để tứ giác MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì?
c) Cho AC = 6 cm, BD = 8 cm. Hãy tính diện tích tứ giác MNPQ.
Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng:
\(\frac{1}{{{a^3}\left( {b + c} \right)}} + \frac{1}{{{b^3}\left( {c + a} \right)}} + \frac{1}{{{c^3}\left( {a + b} \right)}} \ge \frac{3}{2}\).
Số viên bi của ba bạn Minh, Hùng, Dũng tỉ lệ với các số 2; 4; 5. Tính số viên bi của mỗi bạn biết rằng ba bạn có 44 viên bi.
Cho tam giác ABC (\(\widehat B = 90^\circ \)) có đường cao BD. Gọi E, F lần lượt là trung điểm của BD, DC và H là giao điểm của AE, BF. Tính \(\widehat {AHB}\)?
Cho tập hợp A = {1; 2; 3; 4; 5; 6; 7; 8}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên có 6 chữ số khác nhau và phải có mặt các chữ số 1, 2, 3 sao cho chúng không đứng cạnh nhau?
Chứng minh rằng nếu p là một số nguyên tố thì np – n chia hết cho p với mọi số nguyên dương n.
Cho tam giác ABC có \(\widehat A = 60^\circ \). Các tia phân giác của \(\widehat B\) và \(\widehat C\) cắt nhau ở I, cắt cạnh AC, AB ở D và E. Tia phân giác của \(\widehat {BIC}\) cắt BC ở F.
a) Tính \(\widehat {BIC}\).
b) Chứng minh ID = IE = IF.
c) Chứng minh tam giác DEF đều.
d) Chứng minh I là giao điểm các đường phân giác của hai tam giác ABC và DEF.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, \(BC = a\sqrt 3 \). Tam giác SOA cân tại S và nằm trong mặt phẳng vuông góc với đáy. SC tạo với mặt phẳng đáy một góc 60°. Tính thể tích khối chóp S.ABCD.
