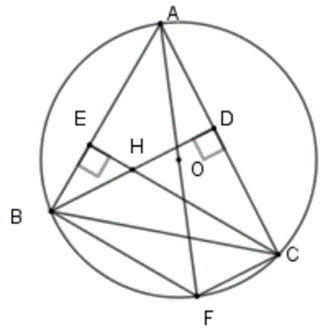
Cho tam giác ABC nội tiếp đường tròn tâm O, hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của BC. Chứng minh 3 điểm H; M; F thẳng hàng.
c) Chứng minh \(OM = \frac{1}{2}AH.\)
 Giải bởi Vietjack
Giải bởi Vietjack
a) \(\widehat {ACF} = 90^\circ \)(chắn nửa đường tròn)
⇒ FC vuông góc với AC
Lại có BH vuông góc với AC
⇒ FC // BH (1)
Chứng minh tương tự: BF // CH (2)
Từ (1) và (2) ⇒ BFCH là hình bình hành.
b) Vì BFCH là hình bình hành nên 2 đường chéo HF và BC giao nhau tại trung điểm mỗi đường.
Mà M là trung điểm của BC ⇒ M đồng thời là trung điểm của HF
⇒ H, M, F thẳng hàng (đpcm)
c) Xét tam giác AHF có O là trung điểm của AF
Có M là trung điểm của HF ⇒ OM là đường trung điểm của tam giác AHF
⇒ \(OM = \frac{1}{2}AH\) (đpcm)
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh CH vuông góc AB.
c) Chứng minh tam giác PIQ cân.
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) \(\Delta AMB = \Delta EMC\).
b) AC ⊥ CE.
c) BC = 2AM.
Cho tam giác ABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.
c) Gọi I là giao điểm của EF và AH, M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.
Cho a là góc tù và \(\sin a = \frac{4}{5}\). Tính A = 2sina – cosa.
Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho \(AM = \frac{{AC}}{4},\) N là trung điểm của đoạn thẳng DC. Tìm mệnh đề đúng?
Cho tam giác ABC, trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. Một đường thẳng đi qua A cắt các cạnh DE và BC theo thứ tự ở M và N. Chứng minh:
a) BC // DE.
b) AM = AN.
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh \(\widehat {ABD} = \widehat {AED}\).
b) Tia ED cắt AB tại F. Chứng minh AC = AF.
c) Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh DI = 2IH.
Cho tam giác ABC đều cạnh a. Gọi M, N là các điểm sao cho \(3\overrightarrow {BM} = 2\overrightarrow {BC} ,5\overrightarrow {AN} = 4\overrightarrow {AC} .\)
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} ,\,\,\overrightarrow {BC} .\overrightarrow {AC} .\)
b) Chứng minh AM vuông góc với BN.
Cho đa thức bậc 2 có dạng P(x) = ax2 + bx + c biết rằng P(x) thỏa mãn 2 điều kiện sau: P(0) = −2 và 4P(x) – P(2x – 1) = 6x – 6. Chứng minh rằng a + b + c = 0 và xác định đa thức P(x).
Cho △ABC nhọn các đường cao AD và BE cắt tại H. Gọi M là trung điểm BC. P đối xứng với H qua BC, Q đối xứng với H qua M.
a) PQ // BC. Tứ giác DMQP là hình gì?
b) Chứng minh rằng: HCQB là hình bình hành.
Cho nửa đường tròn (O; R) đường kính AB. Bán kính OC vuông góc với AB. Gọi d là tiếp tuyến tại A của nửa đường tròn (O). Qua điểm M bất kì thuộc nửa đường tròn (O), kẻ tiếp tuyến với đường tròn cắt d tại E và cắt đường thẳng OC tại D. Gọi F là giao điểm của BD và d. Tiếp tuyến tại B cắt ED tại K. Chứng minh BK = EF.
Một mảnh đất hình chữ nhật có chiều dài là 40m, chiều rộng bằng \(\frac{1}{2}\) chiều dài, trong đó diện tích đất làm nhà chiếm 30%. Tính:
a) Diện tích của mảnh đất đó.
b) Diện tích đất làm nhà là bao nhiêu mét vuông?
Cho hàm số y = (2m – 3)x + m – 1. Chứng minh rằng đồ thị hàm số đi qua điểm cố định với mọi giá trị của m. Tìm điểm cố định ấy.
Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE. Chứng minh:
a) \[\Delta ABC = \Delta ADE\].
b) DE = BC và DE // BC.
c) \[\Delta AEN = \Delta ACM\].
d) M, A, N thẳng hàng.