Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).
a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;
b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh ;
c) Chứng minh MI.MK = MP2;
d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Giải bởi Vietjack
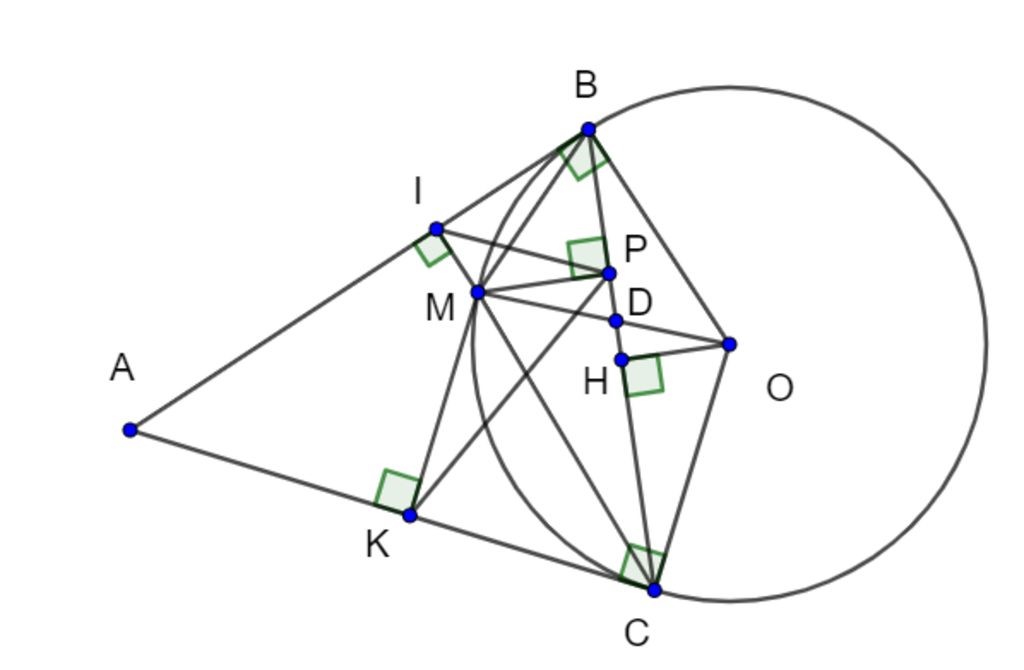
a) Xét tứ giác AIMK có:
= 90° (MI ⊥ AB); = 90° (MK ⊥ AC)
⇒ = 90° + 90° = 180°
Mà 2 góc ở vị trí đối nhau
⇒ Tứ giác AIMK nội tiếp
Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A
⇒ OB ⊥ AB; OC ⊥ AC ⇒ = 90°
Xét tứ giác ABOC có:
= 90° + 90° = 180°
Mà 2 góc ở vị trí đối nhau
⇒ Tứ giác ABOC nội tiếp
b) Xét tứ giác MPCK có:
= 90° (MP ⊥ BC); = 90° (MK ⊥ AC)
⇒ = 90° + 90° = 180°
Mà 2 góc ở vị trí đối nhau
⇒ Tứ giác MPCK nội tiếp
⇒ (cùng nhìn cạnh MK)
Xét (O) có: là góc tạo bởi tiếp tuyến và dây cung MC
là góc nội tiếp chắn cung MC
⇒
Mà ⇒
c) Xét tứ giác MIBP có:
= 90° (MI ⊥ AB) ; = 90°(MP⊥BC)
⇒ = 90° + 90° = 180°
mà 2 góc ở vị trí đối nhau
⇒Ttứ giác MIBP nội tiếp
⇒ (cùng nhìn cạnh MI)
(cùng nhìn cạnh MP) hay
mà ⇒
Xét (O) có: là góc tạo bởi tiếp tuyến và dây cung BM
là góc nội tiếp chắn cung BM
⇒
mà ⇒ hay
Tứ giác MPCK nội tiếp ⇒
⇒
Xét ΔMIP và ΔMPK có:
⇒ ΔMIP ~ ΔMPK (g.g)
⇒ MI.MP = MP.MK ⇒ MI.MK = MP2
d) Vì MI.MK = MP2 nên MI.MK.MP = MP3
Tích MI.MK.MP đạt giá trị lớn nhất khi MP lớn nhất
Gọi H là hình chiếu của O trên BC
⇒ OH cố định (Vì O cố định; BC cố định)
Gọi D là giao điểm của MO và BC
Ta có: MP ≤ MD; OH ≤ OD
MP + OH ≤ MD + OD = MO ⇒ MP + OH ≤ R
⇒MP ≤ R−OH ⇒ MP3 ≤ (R − OH)3
Dấu "=" xảy ra khi MP = R − OH
⇒ O, H, Mthẳng hàng
⇒ M nằm chính giữa cung nhỏ BC
Vậy tích MI.MK.MP đạt giá trị lớn nhất khi M nằm chính giữa cung nhỏ BC.
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 9cm, AC = 12cm. Tính BC, AH, HB, HC, diện tích tam giác ABC.
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Cho tam giác ABC vuông tại A, có đường cao AH. Từ H kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) Cho biết AB = 3cm, = 30°. Tính độ dài các đoạn AC, HA.
b) Chứng minh: BE.BA + CF.CA + 2.HB.HC = BC2.
Cho tam giác ABC. Hai điểm M, N được xác định bởi hệ thức: . Tìm mệnh đề đúng trong các mệnh đề sau: (1) MN và AC song song; (2) MN và AC cắt nhau; (3) MN = AC; (4) 3 điểm M, A, C thẳng hàng
Cho tam giác ABC và ba điểm M, N, P thỏa mãn , , . Chứng minh rằng M, N, P thẳng hàng.
Cho tam giác ABC có đường cao AD, và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh
a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.
b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.
Cho tam giác ABC thỏa mãn . Chứng minh tam giác ABC là tam giác vuông.
Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Xét tính đúng, sai của mệnh đề P và Q?
Cho hình chữ nhật ABCD có AB = 4cm, BC = 3cm. Kẻ BH vuông góc với AC tại H, tia BH cắt AD tại E.
1) Tính BH, góc BAC.
2) Chứng minh: BH.BE = CD2.
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 9cm ; AC=12cm
a) Tính số đo góc B (làm tròn đến độ) và độ dài BH
b) Gọi E, F là hình chiếu của H trên AB, AC. Chứng minh AE.AB = AF.AC.
Lớp 10A chọn ra một số học sinh tham gia làm bài khảo sát học sinh giỏi môn Toán. Đề thi có 3 câu. Sau khi chấm bài giáo viên tổng kết được như sau: Có 5 học sinh làm được câu 1, có 6 học sinh làm được câu 2, có 4 học sinh làm được câu 3. Có 3 học sinh làm được câu 1 và câu 2, có 2 học sinh làm được câu 1 và câu 3, có 1 học sinh làm được câu 2 và câu 3 và chỉ có 1 học sinh làm được cả 3 câu. Hỏi có tất cả bao nhiêu học sinh tham gia làm bài khảo sát?
Cho tam giác ABC nhọn, các đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh: Tam giác ABE và tam giác AFC đồng dạng, AF. AB = AE . AC.
b) Chứng minh = .
c) Cho AE = 3cm, AB = 6cm. Chứng minh: SABC = 4SAEF.
Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại D.
a) Chứng minh tam giác ABD bằng tam giác ADC.
b) Kẻ DH vuông góc với AB (H thuộc AB), DK vuông góc với AC (K thuộc AC). Chứng minh DH = CK.
c) Biết = 4 , tính số đo các góc của tam giác ABC.
Cho đường tròn (O,R) cố định. Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm). Gọi H là giao điểm của OM, AB.
a) Chứng minh: OM vuông góc với AB và OH.OM = R2.
b) Từ M kẻ cát tuyến MNP với đường tròn (O) (N nằm giữa M,P), gọi I là trung điểm NP (I khác O). Chứng minh: A, M, O, I thuộc một đường tròn và tìm tâm của đường tròn đó.
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA, MB theo thứ tự C,D. Biết MA = 5cm, tính chu vi tam giác MCD.
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt MA, MB lần lượt tại E, F. Xác định vị trí của điểm M để diện tích tam giác MEF nhỏ nhất.
Cho tam giác ABC, N là điểm xác định bởi , G là trọng tâm tam giác ABC. Hệ thức tính theo và là?
