Tọa độ điểm cực đại của đồ thị hàm số y = x3 – 3x2 + 4 là:
A. (2; 4)
B. (2; 0)
C. (0; –4)
D. (0; 4).
Giải bởi Vietjack
Đáp án đúng là: D
TXĐ: D = ℝ
Ta có: y’ = 3x2 – 6x
\(y' = 0 \Leftrightarrow 3{{\rm{x}}^2} - 6{\rm{x}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Ta có bảng biến thiên
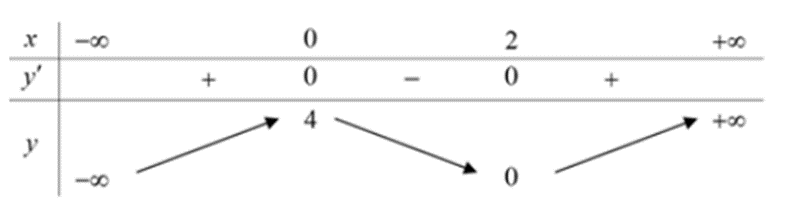
Dựa vào bảng biến thiên ta thấy tọa độ điểm cực đại là (0; 4)
Vậy ta chọn đáp án D.
Từ một điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MP và MQ với đường tròn (P, Q là tiếp điểm) và 1 cát tuyến MAB (A nằm giữa M và B). Gọi I là trung điểm của AB.
a) Chứng minh 5 điểm M, P, O, I, Q cùng thuộc 1 đường tròn.
b) PQ cắt AB tại E. Chứng minh MP2 = ME . MI.
c) Qua A kẻ đường thẳng song song MP cắt PQ, PB lần lượt tại H và K. Chứng minh KB = 2HI.
Thiết diện qua trục của một hình trụ là hình vuông có chu vi là 8a. Diện tích xung quanh của hình trụ đó là:
Trong số 50 học sinh của lớp 10A có 15 bạn đucợ xếp loại học lực giỏi, 25 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa được học sinh giỏi vừa được hạnh kiểm tốt. Khi đó lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạnd dó phải có học lực giỏi hay hạnh kiểm tốt.
Hàm số \(F\left( x \right) = {e^{{x^2}}}\) là nguyên hàm của hàm số nào trong các hàm số sau:
Chứng minh rằng trong tam giác ABC, ta có:
tanA + tanB + tanC = tanA.tanB.tanC \(\left( {\widehat A,\widehat B,\widehat C \ne \frac{\pi }{2}} \right)\).
Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?
Cho hình vuông ABCD, M là một điểm nằm giữa B và C. Kẻ AN vuông góc với AM, AP vuông góc với MN (N và P thuộc đường thẳng CD).
a) Chứng minh tam giác AMN vuông cân và AN2 = NC . NP
b) Tính tỉ số chu vi tam giác CMP và chu vi hình vuông ABCD.
c) Gọi Q là giao điểm của tia AM và tia DC. Chứng minh tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC.
