Cho đường tròn (O; R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B.
a) Chứng minh tứ giác ABHM nội tiếp.
b) Chứng minh OA.OB = OH.OM = R2.
Giải bởi Vietjack
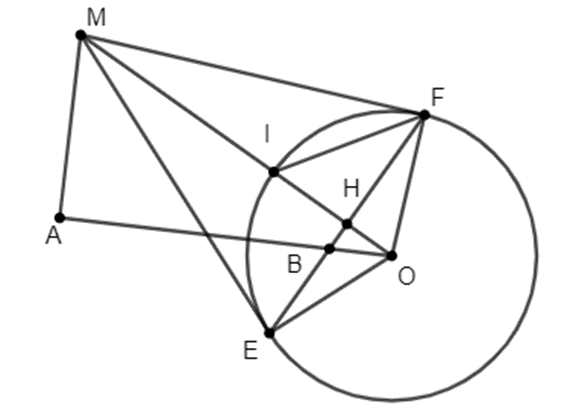
a) Do ME, MF là tiếp tuyến với đường tròn suy ra ME = MF nên M thuộc đường trung trực của EF.
Ta có OE = OF nên O thuộc đường trung trực của EF.
Do đó OM là đường trung trực của EF.
⇒ EF ⊥ OM.
Tứ giác ABHM có \(\widehat {BAM} = \widehat {BHM} = 90^\circ \), mà hai góc này ở vị trí đối nhau nên tứ giác này nội tiếp đường tròn bán kính MB.
b) Xét ∆OHB và ∆OAM có:
\(\widehat {OHB} = \widehat {OAM} = 90^\circ \); \(\widehat {MOA}\) chung
(g.g)
\( \Rightarrow \frac{{OH}}{{OA}} = \frac{{OB}}{{AM}}\)
⇒ OA.OB = OH.OM (1)
Xét ∆OHE và ∆OEM có:
\(\widehat {OHE} = \widehat {OEM} = 90^\circ \); \(\widehat {MOE}\) chung
Do đó (g.g)
Suy ra \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OM}}\)
Hay OH.OM = OE2 (2)
Từ (1) và (2) suy ra OA.OB = OH.OM = OE2 = R2.
Cho hình nón (N) có đỉnh S, bán kinh đáy bằng \(\sqrt 3 a\) và độ dài đường sinh bằng 4a. Gọi (T) là mặt cầu đi qua S và đường tròn đáy của (N). Bán kính của (T) bằng:
Bạn An ra nhà sách và mang theo một số tiền vừa đủ để mua 10 quyển tập và 6 cây bút. Nhưng khi ra đến nơi, giá một quyển tập mà bạn An định mua đã tăng lên 500 đồng một quyển tập, còn giá một cây bút thì giảm 1000 đồng một cây so với dự định. Vậy để mua 10 quyển tập và 6 cây bút như trên thì bạn An còn thừa hay thiếu số tiền là bao nhiêu?
Gọi điểm M là điểm thuộc cạnh BC của tam giác ABC sao cho BM = 3MC. Khi đó \(\overrightarrow {AM} \) bằng
Cho đường tròn tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME < MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm, A nằm giữa hai điểm M và B, A và C nằm khác phía đối với đường thẳng MO).
a) Chứng minh MA.MB = ME.MF.
b) Gọi H là hình chiếu vuông góc của điểm C lên đường thẳng MO. Chứng minh tứ giác AHOB nội tiếp.
Cho hàm số y = x4 + 8x2 + m có giá trị nhỏ nhất trên [1; 3] bằng 6. Tham số thực m bằng
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn \(\overrightarrow {MA} \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) là
Cho hàm số y = x4 – 2mx2 + m. Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị:
Một lớp có 45 học sinh trong đó có 20 nam. Có bao nhiêu cách chọn ra một ban cán sự gồm 4 học sinh nếu có ít nhất 1 học sinh nam?
Cho một hình lập phương ABCDEFGH có các cạnh đều bằng nhau và bằng 7cm. Hỏi thể tích hình lập phương ABCDEFGH bằng bao nhiêu?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\) là:
Cho lăng trụ ABCD.A’B’C’D’ có ABCD là hình chữ nhật có AA’ = A’B = A’D. Tính thể tích của khối lăng trụ ABCD.A’B’C’D’ biết AB = a, \(AD = a\sqrt 3 \), AA’ = 2a.
