Cho hình chữ nhật ABCD, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là đúng?
A. AE là đường vuông góc kẻ từ A đến CD;
B. AE là đường xiên kẻ từ A đến CD;
C. AC là đường vuông góc kẻ từ A đến CD;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B
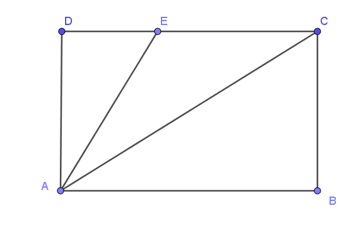
Do ABCD là hình chữ nhật nên AD vuông góc với CD tại D.
Do đó AD là đường vuông góc kẻ từ A đến CD, vậy phương án D sai.
Lại có, E nằm giữa C và D nên AE là đường xiên kẻ từ A đến CD, vậy phương án A sai và phương án B đúng.
Ta có AC không vuông góc với CD nên AC là đường xiên kẻ từ A đến CD, vậy phương án C sai.
Vậy ta chọn phương án B.
Cho tam giác ABC vuông tại B có AD là tia phân giác của góc BAC (D ∈ BC). Biết BD = 3 cm. Khoảng cách từ D đến đường thẳng AC bằng
Cho hình thang cân ABCD có đáy nhỏ AB = 4 cm, đáy lớn CD = 7 cm. Biết diện tích hình thang bằng 22 cm2, khoảng cách giữa hai đáy AB và CD bằng:
Cho Ot là tia phân giác của góc đó. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho (A, B không trùng O). Kẻ AH, BK vuông góc Ot. Gọi I là giao điểm của AB và HK như hình vẽ:
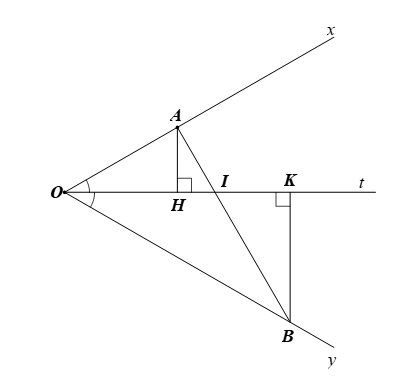
Có bao nhiêu đường vuông góc trong hình vẽ trên?
Cho hình vẽ dưới đây:
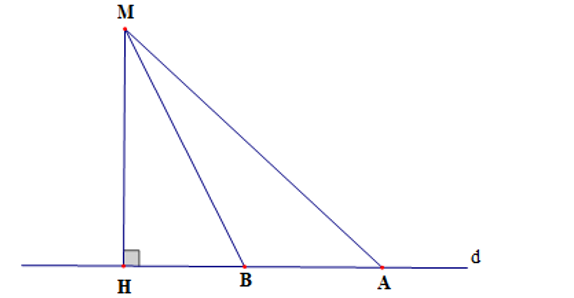
Số đường xiên kẻ từ điểm M đến đường thẳng d là:
Cho hình chữ nhật NMQP có MN = 2 cm, MQ = 5 cm. Khoảng cách từ P đến MN và MQ lần lượt là:
Cho tam giác ABC đều cạnh 4 cm. Biết khoảng cách từ A đến cạnh BC bằng cm. Khoảng cách từ B đến AC là
Cho hình vẽ dưới đây:
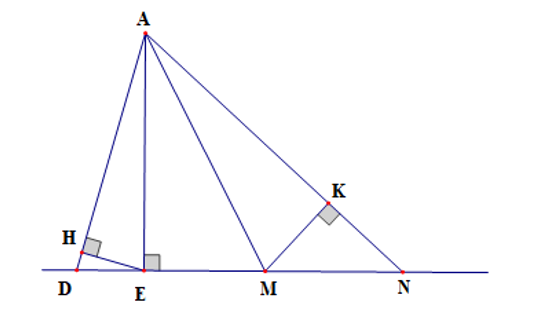
Số đường vuông góc kẻ từ điểm A có trong hình vẽ là: