9 câu hỏi trắc nghiệm thuộc Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng

Trắc nghiệm Toán 7 Bài 32. Quan hệ giữa đường vuông góc và đường xiên có đáp án

Dạng 1. Nhận biết đường vuông góc, đường xiên. Tìm khoảng cách của một điểm đến một đường thẳng

126 lượt thi
9 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình vẽ dưới đây:

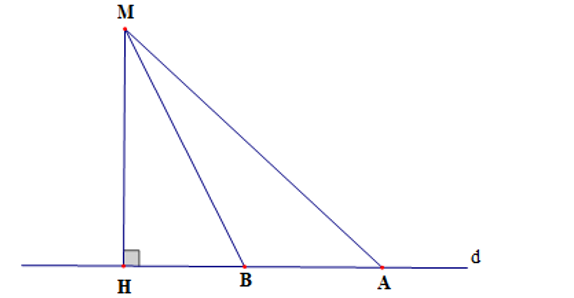
Số đường xiên kẻ từ điểm M đến đường thẳng d là:

A. 1;

B. 2;

C. 3;

D. 4.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có: MA và MB là hai đường xiên kẻ từ điểm M đến đường thẳng d.

Vậy ta chọn đáp án B.

Câu 2:

Cho hình vẽ dưới đây:

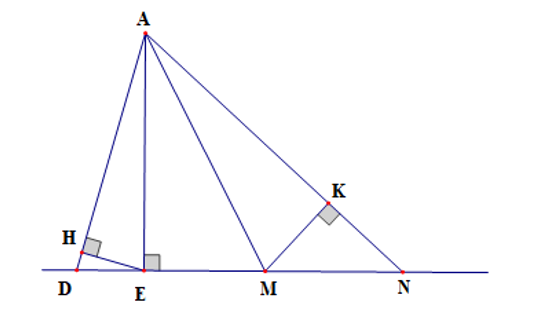
Số đường vuông góc kẻ từ điểm A có trong hình vẽ là:

A. 1;

B. 2;

C. 3;

D. 4.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có AH, AE, AK lần lượt là các đường vuông góc kẻ từ điểm A đến đoạn thẳng HE, DN, MK. Do đó có 3 đường vuông góc kẻ từ điểm A có trong hình vẽ.

Vậy ta chọn đáp án C.

Câu 3:

Cho hình chữ nhật ABCD, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là đúng?

A. AE là đường vuông góc kẻ từ A đến CD;

B. AE là đường xiên kẻ từ A đến CD;

C. AC là đường vuông góc kẻ từ A đến CD;

D. AD là đường xiên kẻ từ A đến CD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

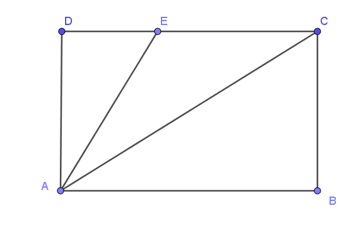
Cho hình chữ nhật ABCD, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là đúng? (ảnh 1)

Do ABCD là hình chữ nhật nên AD vuông góc với CD tại D.

Do đó AD là đường vuông góc kẻ từ A đến CD, vậy phương án D sai.

Lại có, E nằm giữa C và D nên AE là đường xiên kẻ từ A đến CD, vậy phương án A sai và phương án B đúng.

Ta có AC không vuông góc với CD nên AC là đường xiên kẻ từ A đến CD, vậy phương án C sai.

Vậy ta chọn phương án B.

Câu 4:

Cho tam giác ABC vuông tại B có AD là tia phân giác của góc BAC (D ∈ BC). Biết BD = 3 cm. Khoảng cách từ D đến đường thẳng AC bằng

A. 3 cm;

B. 6 cm;

C. 1,5 cm;

D. 2 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

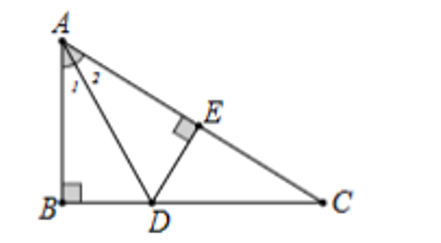
Cho tam giác ABC vuông tại B có AD là tia phân giác của góc BAC (D ∈ BC). Biết BD = 3 cm. (ảnh 1)

Kẻ DE ⊥ AC khi đó DE là khoảng cách từ D đến AC.

Vì AD là tia phân giác của $\hat{B A C}$ nên ${\hat{A}}_{1} = {\hat{A}}_{2} .$

Xét tam giác ABD và tam giác AED có:

$\hat{B} = \hat{A ED} (= 90 °);$

AD là cạnh chung;

${\hat{A}}_{1} = {\hat{A}}_{2}$ (chứng minh trên).

Suy ra ∆ABD = ∆AED (cạnh huyền – góc nhọn).

Do đó BD = ED (2 cạnh tương ứng).

Mà BD = 3 cm nên DE = 3 cm.

Vậy ta chọn phương án A.

Câu 5:

Cho hình chữ nhật NMQP có MN = 2 cm, MQ = 5 cm. Khoảng cách từ P đến MN và MQ lần lượt là:

A. 2 cm và 2 cm;

B. 2 cm và 5 cm;

C. 5 cm và 2 cm;

D. 5 cm và 5 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

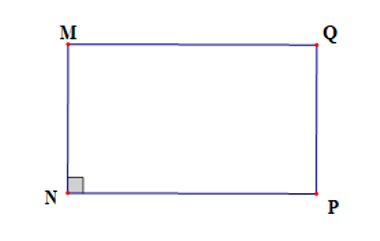
Cho hình chữ nhật NMQP có MN = 2 cm, MQ = 5 cm. Khoảng cách từ P đến MN và MQ lần lượt là: (ảnh 1)

Vì MNPQ là hình chữ nhật nên PQ ⊥ MQ và PN ⊥ MN.

Do đó PQ là khoảng cách từ P đến MQ và PN là khoảng cách từ P đến MN.

Lại có PQ = MN = 2 cm, PN = MQ = 5 cm.

Vậy ta chọn phương án C.

Câu 6:

Trong các phát biểu sau, phát biểu nào đúng?

A. Từ một điểm nằm ngoài một đường thẳng chỉ kẻ được một đường xiên duy nhất đến đường thẳng đó;

B. Từ một điểm nằm ngoài một đường thẳng kẻ được vô số đường vuông góc đến đường thẳng đó;

C. Khi một điểm A nằm trên đường thẳng d thì khoảng cách từ A đến d khác 0;

D. Khi một điểm A nằm trên đường thẳng d thì khoảng cách từ A đến d bằng 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

⦁ Từ một điểm nằm ngoài một đường thẳng chỉ kẻ được duy nhất một đường vuông góc và vô số đường xiên đến đường thẳng đó. Do đó phương án A, B sai.

⦁ Khi một điểm A nằm trên đường thẳng d thì khoảng cách từ A đến d bằng 0. Do đó phương án C sai và D đúng.

Vậy ta chọn phương án D.

Câu 7:

Cho tam giác ABC đều cạnh 4 cm. Biết khoảng cách từ A đến cạnh BC bằng $2 \sqrt{3}$ cm. Khoảng cách từ B đến AC là

A. 4 cm;

B. 2 cm;

C. $\sqrt{3}$ cm;

2 \sqrt{3}

cm.

Xem đáp án

Cho tam giác ABC đều cạnh 4 cm. Biết khoảng cách từ A đến cạnh BC bằng 2 căn bậc hai 3 cm. Khoảng cách từ B đến AC là (ảnh 1)

Câu 8:

Cho $\hat{x O y} = 60 °,$ Ot là tia phân giác của góc đó. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho $\hat{A B O} = 30 °$ (A, B không trùng O). Kẻ AH, BK vuông góc Ot. Gọi I là giao điểm của AB và HK như hình vẽ:

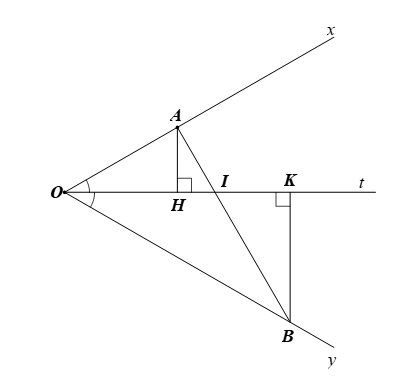
Cho góc xOy= 60 độ , Ot là tia phân giác của góc đó. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho (ảnh 1)

Có bao nhiêu đường vuông góc trong hình vẽ trên?

A. 1;

B. 2;

C. 3;

D. 4.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

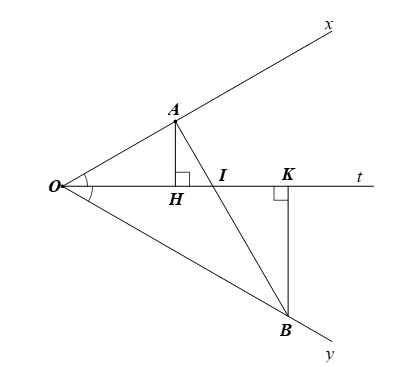
Cho góc xOy= 60 độ , Ot là tia phân giác của góc đó. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho (ảnh 2)

Vì AH, BK vuông góc với Ot nên có 1 đường vuông góc kẻ từ A đến Ot và 1 đường vuông góc kẻ từ B đến Ot.

Xét ∆AOB có $\hat{O A B} + \hat{O B A} + \hat{A O B} = 180 °$ (tổng ba góc trong một tam giác)

Hay $\hat{O A B} + 30 ° + 60 ° = 180 °$

Suy ra $\hat{O A B} = 90 °$ nên AB ⊥ Ox. Khi đó BA là 1 đường vuông góc kẻ từ B đến Ox.

Vậy có 3 đường vuông góc trong hình vẽ trên, ta chọn phương án C.

Câu 9:

Cho hình thang cân ABCD có đáy nhỏ AB = 4 cm, đáy lớn CD = 7 cm. Biết diện tích hình thang bằng 22 cm², khoảng cách giữa hai đáy AB và CD bằng:

A. 4 cm;

B. 7 cm;

C. 12 cm;

D. 8 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

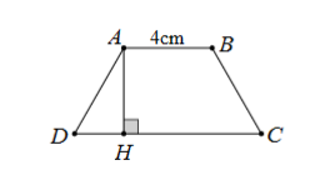
Cho hình thang cân ABCD có đáy nhỏ AB = 4 cm, đáy lớn CD = 7 cm. Biết diện tích hình thang bằng (ảnh 1)

Kẻ AH ⊥ CD khi đó AH là đường cao của hình thang cân ABCD

Mà ABCD là hình thang cân nên AB // CD nên độ dài đoạn thẳng AH là khoảng cách giữa hai đáy AB và CD.

Diện tích hình thang ABCD bằng 22 cm² nên ta có $\frac{(A B + C D) . A H}{2} = 22$

Hay $\frac{(4 + 7) . A H}{2} = 22$

Suy ra AH = 4 cm.

Vậy ta chọn phương án A.

Bắt đầu thi ngay