Trắc nghiệm Toán 7 Bài 32. Quan hệ giữa đường vuông góc và đường xiên có đáp án
Dạng 2. Quan hệ giữa đường vuông góc và đường xiên
-
125 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ dưới đây
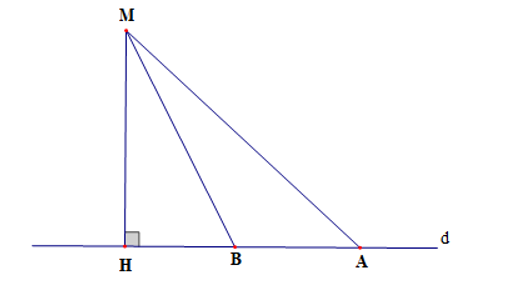
Đoạn thẳng nào có độ dài ngắn nhất trong các đoạn thẳng MH, MB, MA?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Ta thấy MH là đường vuông góc, MA và MB là các đường xiên kẻ từ M đến d.
Do đó độ dài MH là ngắn nhất.
Vậy ta chọn phương án A.
Câu 3:
Cho tam giác ABC đường cao AH, BK. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
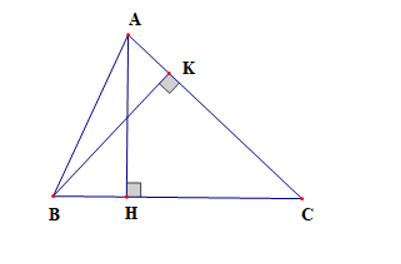
Vì AH là đường vuông góc, AC là đường xiên kẻ từ A đến BC nên AH < AC.
Vì BK là đường vuông góc, BC là đường xiên kẻ từ B đến AC nên BK < BC.
Suy ra AH + BK < AC + BC.
Vậy ta chọn phương án B.
Câu 4:
Bạn Hoa tập chạy theo các tuyến đường AB, AC, AD, AE, AF như hình vẽ:
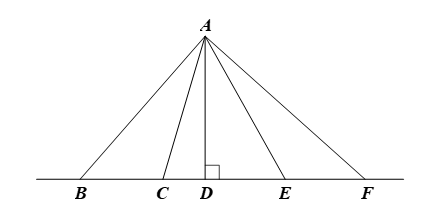
Biết với cùng vận tốc như nhau, Hoa chạy đoạn đường AB mất 15 phút, chạy đoạn AF mất 20 phút. Nếu Hoa chạy đoạn đường AD thì khoảng thời gian nào sau đây là hợp lí nhất?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Ta thấy AD là đường vuông góc, AB, AC, AD và AF là các đường xiên nên AD là đường ngắn nhất.
Suy ra thời gian chạy đoạn đường AD là ngắn nhất.
Do đó thời gian Hoa chạy đoạn đường AD nhỏ hơn 15 phút.
Vậy ta chọn phương án A.
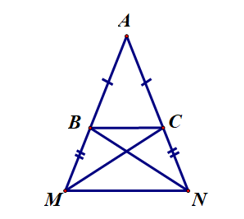
Câu 5:
Cho tam giác ABC cân tại A. Đường cao AH. Lấy điểm M tùy ý trên cạnh BC. Độ dài AM nhỏ nhất khi
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
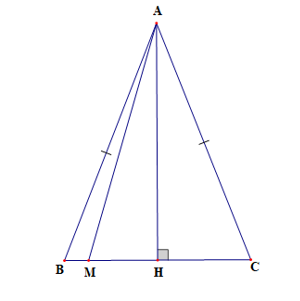
Xét tam giác ABC có AH là đường cao nên AH ⊥ BC.
Suy ra AH là đường vuông góc kẻ từ A đến BC nên AH là đường ngắn nhất trong tam giác ABC.
Suy ra khi M trùng H thì AM nhỏ nhất.
Vậy ta chọn phương án C.
Câu 6:
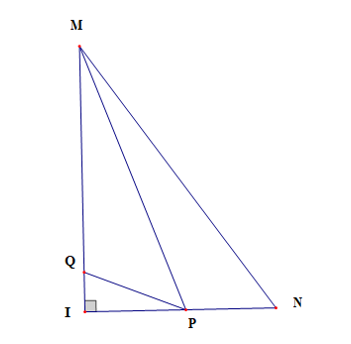
Cho tam giác IMN. Trên MN lấy E (IE không vuông góc với MN). Kẻ MP, NQ vuông góc IE. Cho các khẳng định sau:
(I) MP > ME.
(II) MN > MP + NQ.
(III) EN > NQ.
(IV) IQ < IN.
(V) IM < MP.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
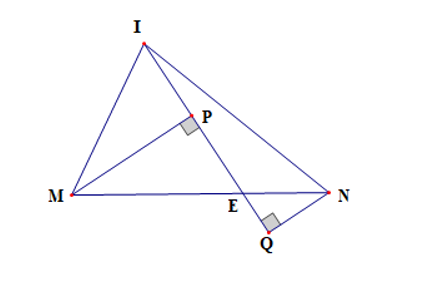
⦁ Ta có MP là đường vuông góc, MI và ME là các đường xiên kẻ từ M đến IQ nên MP < MI, MP < ME.
Do đó khẳng định (I) và (V) là sai.
⦁ Ta có IQ là đường vuông góc, IN là đường xiên kẻ từ I đến NQ nên IQ < IN.
Do đó khẳng định (IV) là đúng.
⦁ Ta có NQ là đường vuông góc, NE là đường xiên kẻ từ N đến EQ nên NQ < NE
Do đó khẳng định (III) là đúng.
⦁ Ta có: MN = ME + EN
Mà MP < ME, NQ < NE
Suy ra MP + NQ < ME + EN = MN.
Do đó khẳng định (II) là đúng.
Vậy có 3 khẳng định đúng, ta chọn phương án C.
Câu 7:
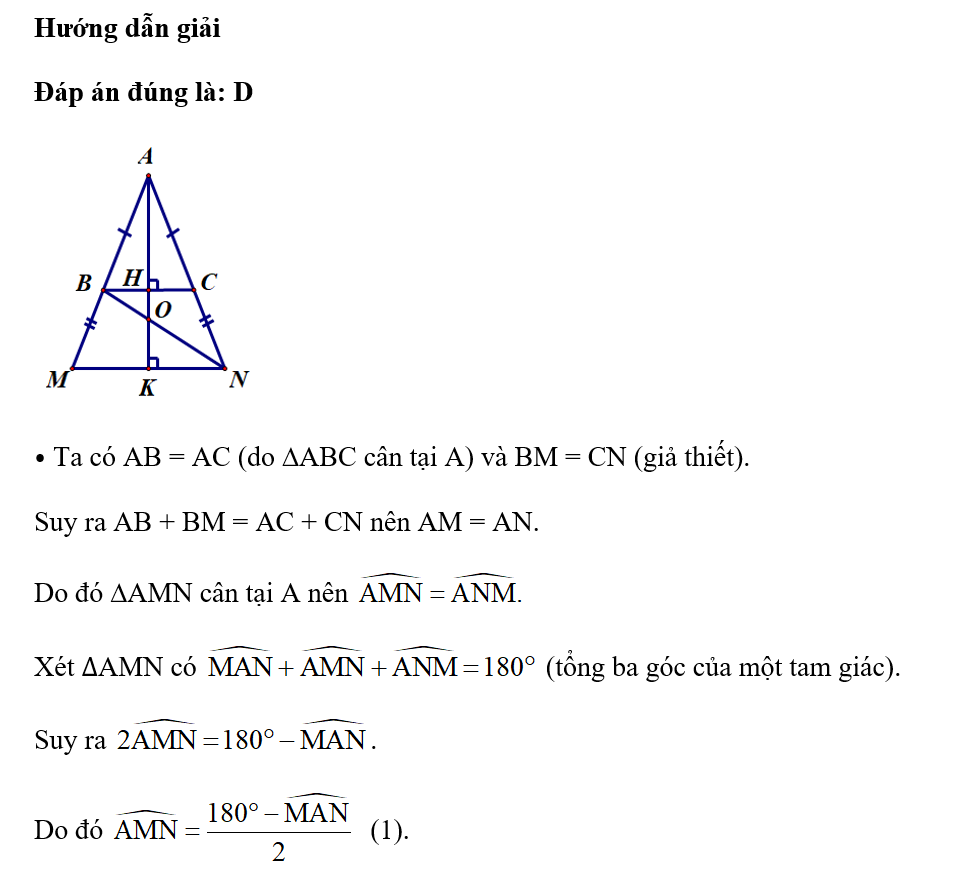
Cho hình vẽ sau:
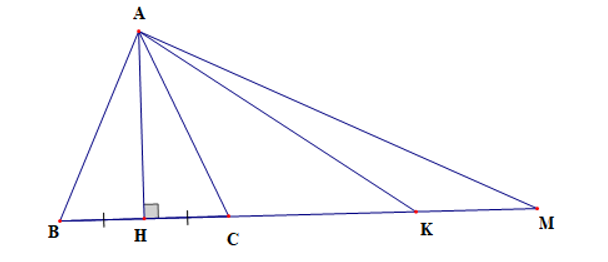
Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
⦁ Xét tam giác ABH và tam giác AHC có:
AH là cạnh chung;
BH = CH (giả thiết)
Suy ra ΔABH = ΔACH (hai cạnh góc vuông).
Do đó AB = AC (hai cạnh tương ứng). Do đó khẳng định A là đúng.
⦁ Vì AH là đường vuông góc, AC và AK là các đường xiên kẻ từ A đến đường thẳng BM nên AH < AC, AH < AK. Do đó khẳng định D đúng, khẳng định C sai.
⦁ Xét ∆AKM có nên là góc tù.
Do đó cạnh AM là lớn nhất nên AK < AM. Do đó khẳng định B đúng.
Vậy ta chọn phương án C.
Câu 8:
Cho tam giác MNE vuông tại E, A là trung điểm của EM. Gọi H, K lần lượt là hình chiếu của E, M trên AN. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
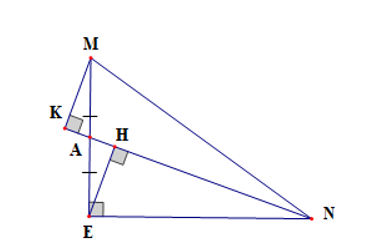
⦁ Xét tam giác AKM và tam giác AHE có
AM = AE (do A là trung điểm của ME);
(đối đỉnh)
Suy ra ΔAKM = ΔAHE (cạnh huyền – góc nhọn).
Do đó AH = AK (hai cạnh tương ứng).
⦁ Vì NE, NA lần lượt là đường vuông góc, đường xiên kẻ từ N đến ME nên NE < NA.
Mà NA = NH + HA suy ra NE < NH + HA (1)
Mặt khác, NA = NK – AK
Suy ra NE < NK – AK (2)
Cộng hai vế của (1) và (2) ta được: 2NE < NH + HA + NK – AK.
Suy ra 2NE < NH + NK + AK – AK
Hay 2NE < NH + NK
Vậy ta chọn phương án B.
Câu 9:
Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC. So sánh BC và tổng DH + DK ta được
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
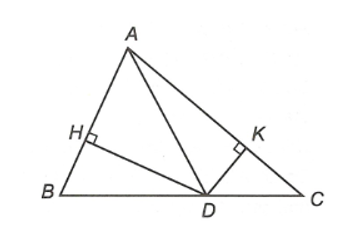
Ta có DH, DB lần lượt là đường vuông góc, đường xiên kẻ từ điểm D đến đường thẳng AB nên DH < DB (1).
Tương tự, ta có DK, DC lần lượt là đường vuông góc, đường xiên kẻ từ điểm D đến đường thẳng AC nên DK < DC (2).
Từ (1), (2), ta suy ra DH + DK < DB + DC = BC.
Khi đó ta có DH + DK < BC.
Vậy ta chọn phương án B.
