Trắc nghiệm Toán 7 KNTT Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng có đáp án
Dạng 1: Vận dụng định nghĩa, tính chất của tam giác cân để chứng minh tính chất khác có đá án
-
575 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho ∆ABC cân tại A, M là trung điểm BC. Gọi D, E lần lượt là hình chiếu của M trên AB và AC. Kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
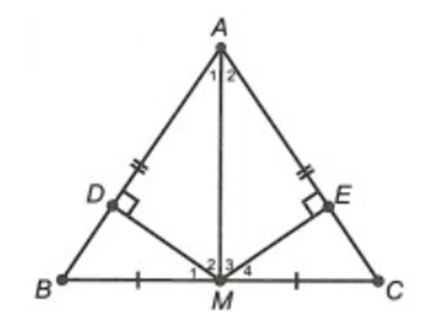
Xét ∆BDM và ∆CEM, có:
\[\widehat {BDM} = \widehat {CEM} = 90^\circ \].
\[\widehat {DBM} = \widehat {ECM}\] (∆ABC cân tại A).
MB = MC (M là trung điểm BC).
Do đó ∆BDM = ∆CEM (cạnh huyền – góc nhọn).
Suy ra BD = CE và \[\widehat {BMD} = \widehat {CME}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án A, C đúng.
Xét ∆ADM và ∆AEM, có:
\[\widehat {ADM} = \widehat {AEM} = 90^\circ \].
AM là cạnh chung.
DM = EM (∆BDM = ∆CEM).
Do đó ∆ADM = ∆AEM (cạnh huyền – cạnh góc vuông).
Suy ra AD = AE (cặp cạnh tương ứng).
Do đó đáp án B đúng.
Vậy ta chọn đáp án D.
Câu 2:
Cho ∆ABC cân tại A. Lấy các điểm D, E theo thứ tự thuộc các cạnh AB, AC sao cho AD = AE. Kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
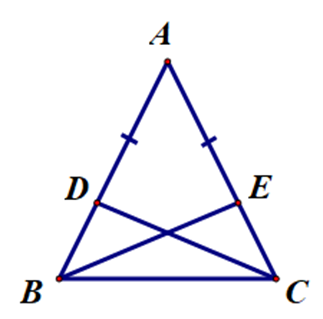
Ta xét từng đáp án:
+ Đáp án B, D:
Vì ∆ABC cân tại A nên ta có AB = AC và \[\widehat {ABC} = \widehat {ACB}\].
Xét ∆ABE và ∆ACD, có:
\[\widehat {BAC}\] là góc chung.
AB = AC (chứng minh trên).
AD = AE (giả thiết).
Do đó ∆ABE = ∆ACD (cạnh – góc – cạnh).
Suy ra BE = CD và \[\widehat {ABE} = \widehat {ACD}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án B đúng, đáp án D sai.
Đến đây ta có thể chọn đáp án B.
+ Đáp án C:
Ta có A, D, B thẳng hàng. Suy ra BD = AB – AD.
Ta có A, E, C thẳng hàng. Suy ra EC = AC – AE.
Ta có AB = AC (chứng minh trên) và AD = AE (giả thiết).
Suy ra AB – AD = AC – AE.
Do đó BD = EC.
Do đó đáp án C sai.
+ Đáp án A:
Xét ∆BDC và ∆CEB, có:
BC là cạnh chung.
BD = EC (chứng minh trên).
\[\widehat {DBC} = \widehat {ECB}\] (chứng minh trên).
Do đó ∆BDC = ∆CEB (cạnh – góc – cạnh).
Suy ra \[\widehat {BDC} = \widehat {CEB}\] (cặp góc tương ứng).
Do đó đáp án A sai.
Vậy ta chọn đáp án B.
Câu 3:
Cho ∆ABC cân tại A. Gọi M, N lần lượt là trung điểm của AC và AB. Cho các khẳng định sau:
(I) ∆ABM = ∆ACN.
(II) ∆BMC = ∆CNB.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
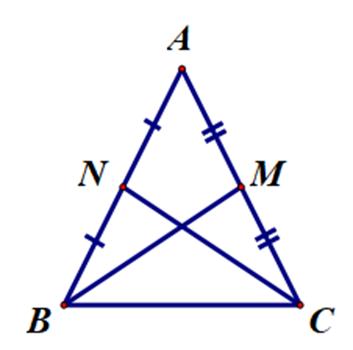
Ta có M là trung điểm AC (giả thiết).
Do đó AC = 2AM = 2CM (1).
Ta có N là trung điểm AB (giả thiết).
Do đó AB = 2AN = 2BN (2).
Vì ∆ABC cân tại A nên AB = AC (3).
Từ (1), (2), (3), ta suy ra AM = AN = CM = BN.
Xét ∆ABM và ∆ACN, có:
AB = AC (∆ABC cân tại A).
\[\widehat {BAC}\] là góc chung.
AM = AN (chứng minh trên).
Do đó ∆ABM = ∆ACN (cạnh – góc – cạnh).
Suy ra (I) đúng.
Xét ∆BMC và ∆CNB, có:
BC là cạnh chung.
CM = BN (chứng minh trên).
\[\widehat {NBC} = \widehat {MBC}\] (∆ABC cân tại A).
Do đó ∆BMC = ∆CNB (cạnh – góc – cạnh).
Suy ra (II) đúng.
Vậy ta chọn đáp án D.
Câu 4:
Cho ∆ABC có \[\widehat A = 100^\circ \] và \[\widehat B = \widehat C\]. Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
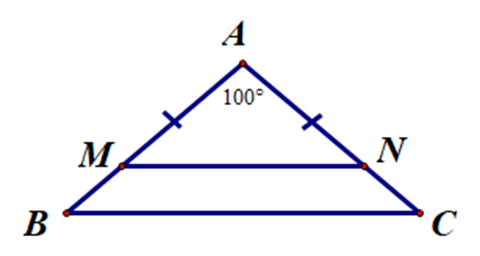
Vì AM = AN nên ∆AMN cân tại A.
Suy ra \[\widehat {AMN} = \widehat {ANM}\].
Do đó đáp án D sai.
Xét ∆AMN, có: \[\widehat {MAN} + \widehat {AMN} + \widehat {ANM} = 180^\circ \].
Suy ra \[2\widehat {AMN} = 180^\circ - \widehat {MAN} = 180^\circ - 100^\circ = 80^\circ \].
Do đó \[\widehat {AMN} = 40^\circ \].
Xét ∆ABC, có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC} = 180^\circ - 100^\circ = 80^\circ \].
Do đó \[\widehat {ABC} = 40^\circ \].
Ta suy ra \[\widehat {AMN} = \widehat {ABC} = 40^\circ \].
Mà hai góc này ở vị trí đồng vị.
Suy ra MN // BC.
Do đó đáp án A đúng.
Vì ba điểm A, B, C tạo thành một tam giác và MN // BC.
Nên MN không song song với AB và MN không song song với AC.
Do đó đáp án B, C sai.
Vậy ta chọn đáp án A.
Câu 5:
Cho ∆ABC cân tại A có \[\widehat A < 90^\circ \]. Kẻ BD ⊥ AC. Trên cạnh AB lấy điểm E sao cho AE = AD. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
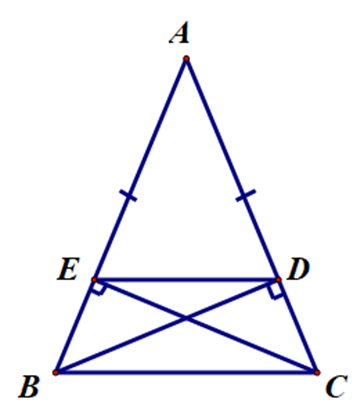
Vì ∆ABC cân tại A nên AB = AC.
Mà AE = AD (giả thiết).
Do đó AB – AE = AC – AD.
Suy ra EB = DC.
Xét ∆CBE và ∆BCD, có:
BC là cạnh chung.
EB = DC (chứng minh trên).
\[\widehat {EBC} = \widehat {DCB}\] (∆ABC cân tại A).
Do đó ∆CBE = ∆BCD (cạnh – góc – cạnh).
Suy ra \[\widehat {CEB} = \widehat {BDC} = 90^\circ \] (cặp góc tương ứng).
Khi đó ta có CE ⊥ BE hay CE ⊥ AB.
Do đó đáp án C đúng.
Vì A, B, C tạo thành một tam giác và CE ⊥ AB.
Nên CE không vuông góc với BC và CE không vuông góc với AC.
Do đó đáp án B, D sai.
∆ADE có AE = AD.
Suy ra ∆ADE cân tại A.
Do đó \[\widehat {AED} = \widehat {ADE}\].
∆ADE có: \[\widehat {BAC} + \widehat {AED} + \widehat {ADE} = 180^\circ \].
Suy ra \[2\widehat {AED} = 180^\circ - \widehat {BAC}\] (1).
∆ABC có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC}\] (2).
Từ (1), (2), ta suy ra \[\widehat {AED} = \widehat {ABC}\].
Mà hai góc này ở vị trí đồng vị.
Do đó DE // BC.
Suy ra đáp án A sai.
Vậy ta chọn đáp án C.
Câu 6:
Cho ∆ABC cân tại A. Trên tia đối của tia AB và AC lấy điểm D và E sao cho AD = AE. Vẽ đường trung tuyến AM của ∆ABC. Tia đối của tia AM cắt DE tại H. Kết luận nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
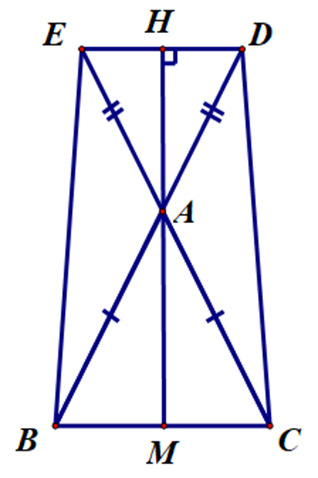
Xét ∆ABE và ∆ACD, có:
AB = AC (∆ABC cân tại A).
AE = AD (giả thiết).
\[\widehat {BAE} = \widehat {CAD}\] (hai góc đối đỉnh).
Do đó ∆ABE = ∆ACD (cạnh – góc – cạnh).
Suy ra EB = DC và \[\widehat {BEA} = \widehat {CDA}\] (cặp cạnh và cặp góc tương ứng).
Do đó đáp án A sai, đáp án C đúng.
Đến đây ta có thể chọn đáp án A.
Xét ∆ABM và ∆ACM, có:
AB = AC (∆ABC cân tại A).
BM = CM (AM là đường trung tuyến của ∆ABC).
\[\widehat {ABM} = \widehat {ACM}\] (∆ABC cân tại A).
Do đó ∆ABM = ∆ACM (cạnh – góc – cạnh).
Suy ra \[\widehat {BAM} = \widehat {CAM}\] (cặp góc tương ứng).
Lại có \[\widehat {BAM} = \widehat {DAH}\] (hai góc đối đỉnh) và \[\widehat {HAE} = \widehat {CAM}\] (hai góc đối đỉnh).
Suy ra \[\widehat {HAE} = \widehat {DAH}\].
Do đó đáp án D đúng.
Vì AD = AE (giả thiết).
Nên ∆ADE cân tại A.
Xét ∆DAH và ∆HAE, có:
AD = AE (giả thiết).
\[\widehat {AEH} = \widehat {ADH}\] (∆ADE cân tại A).
\[\widehat {HAE} = \widehat {DAH}\] (chứng minh trên).
Do đó ∆DAH = ∆HAE (góc – cạnh – góc).
Suy ra \[\widehat {AHE} = \widehat {AHD}\] (cặp góc tương ứng).
Lại có: \[\widehat {AHE} + \widehat {AHD} = 180^\circ \] (hai góc kề bù).
Do đó \[\widehat {AHE} = \widehat {AHD} = 90^\circ \].
Do đó đáp án B đúng.
Vậy ta chọn đáp án A.
Câu 7:
Cho ∆ABC cân tại A có \[\widehat A = 36^\circ \]. Tia phân giác \[\widehat B\] cắt cạnh AC tại D. Khẳng định nào sau đây sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
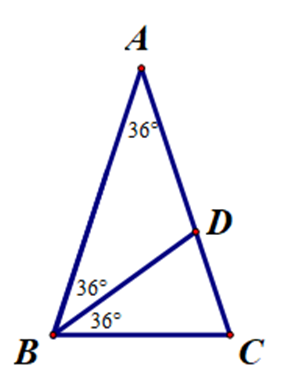
Vì ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
∆ABC có: \[\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \].
Suy ra \[2\widehat {ABC} = 180^\circ - \widehat {BAC} = 180^\circ - 36^\circ = 144^\circ \].
Do đó \[\widehat {BCA} = \widehat {ABC} = 72^\circ \].
Vì BD là phân giác của \[\widehat {ABC}\].
Nên \[\widehat {ABD} = \widehat {DBC} = \frac{{72^\circ }}{2} = 36^\circ \].
Ta có \[\widehat {ABD} = \widehat {BAD} = 36^\circ \].
Nên ∆ABD cân tại D.
Suy ra DA = DB (1).
Do đó đáp án A đúng.
∆ABD cân tại D: \[\widehat {ADB} = 180^\circ - \widehat {ABD} - \widehat {BAD} = 180^\circ - 36^\circ - 36^\circ = 108^\circ \].
Ta có \[\widehat {ADB} + \widehat {BDC} = 180^\circ \] (hai góc kề bù).
Suy ra \[\widehat {BDC} = 180^\circ - \widehat {ADB} = 180^\circ - 108^\circ = 72^\circ \].
Ta có \[\widehat {BDC} = \widehat {BCD} = 72^\circ \].
Suy ra ∆BCD cân tại B.
Do đó BD = BC (2).
Do đó đáp án D sai.
Từ (1), (2), ta suy ra DA = DB = BC.
Do đó đáp án B, C đúng.
Vậy ta chọn đáp án D.
Câu 8:
Cho ∆ABC cân tại A, gọi M là trung điểm BC. Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
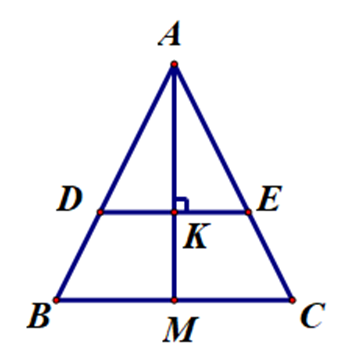
Xét ∆ABM và ∆ACM, có:
AB = AC (∆ABC cân tại A).
\[\widehat {ABM} = \widehat {ACM}\] (∆ABC cân tại A).
BM = CM (M là trung điểm BC).
Do đó ∆ABM = ∆ACM (cạnh – góc – cạnh).
Suy ra \[\widehat {BAM} = \widehat {CAM}\] (cặp góc tương ứng).
Xét ∆ADK và ∆AEK, có:
\[\widehat {AKD} = \widehat {AKE} = 90^\circ \].
AK là cạnh chung.
\[\widehat {DAK} = \widehat {EAK}\] (chứng minh trên).
Do đó ∆ADK = ∆AEK (góc – cạnh – góc).
Suy ra AD = AE và DK = KE (các cặp cạnh tương ứng).
Do đó đáp án B đúng và đáp án A, C, D sai.
Vậy ta chọn đáp án B.
Câu 9:
Cho ∆ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng xy (B, c cùng phía đối với xy). Kẻ BD ⊥ xy, CE ⊥ xy. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
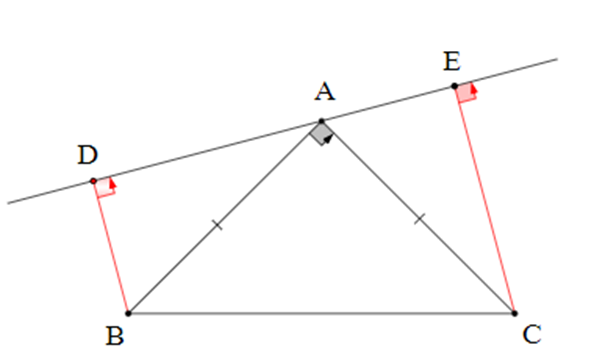
∆ABC vuông tại A. Suy ra \[\widehat {BAC} = 90^\circ \].
Ta có \[\widehat {DAB} + \widehat {BAC} + \widehat {CAE} = 180^\circ \].
Suy ra \[\widehat {DAB} + \widehat {CAE} = 180^\circ - 90^\circ = 90^\circ \].
Xét ∆ABD và ∆CAE, có
\[\widehat {BDA} = \widehat {CEA} = 90^\circ \].
AB = AC (giả thiết).
\[\widehat {DAB} = \widehat {ECA}\] (cùng phụ với \[\widehat {CAE}\]).
Do đó ∆ABD = ∆CAE (cạnh huyền – góc nhọn).
Suy ra DA = EC và DB = EA (các cặp cạnh tương ứng).
Do đó đáp án A, D đúng, đáp án C sai.
Ta có ba điểm D, A, E thẳng hàng và A nằm giữa D, E.
Do đó DE = DA + AE = EC + DB.
Do đó đáp án B đúng.
Vậy ta chọn đáp án C.
Câu 10:
Cho ∆ABC cân tại A. Gọi I là trung điểm BC. Trên cạnh AB lấy điểm D, trên cạnh DI lấy điểm E sao cho I là trung điểm DE. Khẳng định nào sau đây đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
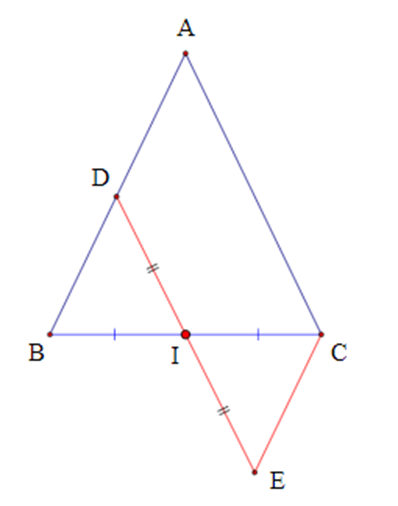
Xét ∆BDI và ∆CEI, có:
BI = CI (I là trung điểm BC).
\[\widehat {BID} = \widehat {CIE}\] (hai góc đối đỉnh).
DI = EI (I là trung điểm DE).
Do đó ∆BDI = ∆CEI (cạnh – góc – cạnh).
Suy ra BD = CE (cặp cạnh tương ứng).
Do đó đáp án A đúng, đáp án C sai.
Ta có ∆BDI = ∆CEI (chứng minh trên).
Suy ra \[\widehat {DBI} = \widehat {ECI}\] (cặp cạnh tương ứng).
Mà \[\widehat {DBI} = \widehat {ACI}\] (∆ABC cân tại A).
Do đó \[\widehat {ECI} = \widehat {ACI}\].
Khi đó CI là tia phân giác \[\widehat {ACE}\].
Hay CB là tia phân giác \[\widehat {ACE}\].
Do đó đáp án B đúng.
Vậy ta chọn đáp án D.
