Trắc nghiệm Toán 7 KNTT Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng có đáp án
Dạng 2; Nhận biết và chứng minh tam giác cân, tam giác đều có đáp án
-
593 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ bên.
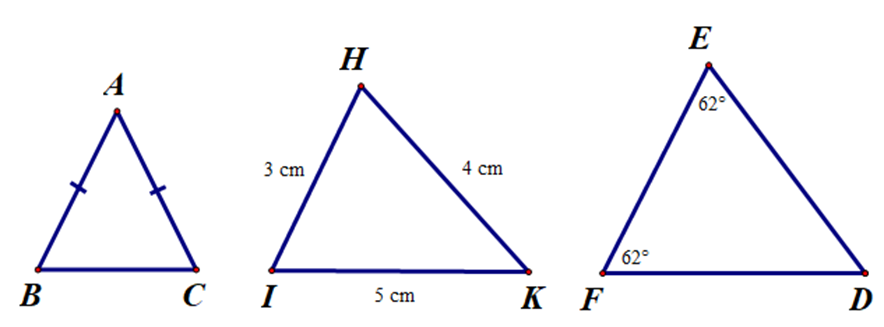
Hình bên có bao nhiêu tam giác cân?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét ∆ABC có: AB = AC (giả thiết).
Suy ra ∆ABC cân tại A.
Xét ∆HIK có: HI ≠ IK ≠ HK (vì 3 cm ≠ 5 cm ≠ 4 cm).
Do đó ∆HIK không phải là tam giác cân.
Xét ∆DEF có: \[\widehat {DEF} = \widehat {DFE} = 62^\circ \].
Suy ra ∆DEF cân tại D.
Khi đó hình trên có 2 tam giác cân là: ∆ABC và ∆DEF.
Vậy ta chọn đáp án C.
Câu 2:
Chọn phát biểu sai trong các phát biểu sau.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đáp án A, B, D đúng.
Đáp án C sai. Sửa lại:
Cách sửa 1: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó có hai góc bằng 60°;
Cách sửa 2: Để nhận biết và chứng minh một tam giác là tam giác đều, ta cần chứng minh tam giác đó là một tam giác cân và có một góc bằng 60°.
Vậy ta chọn đáp án C.
Câu 3:
Cho ∆ABC cân tại A. Trên cạnh BC lấy các điểm M, N sao cho BM = CN. Kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
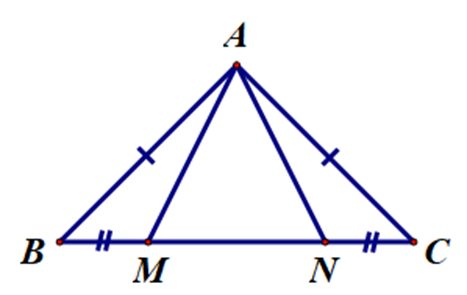
Vì ∆ABC cân tại A nên ta có AB = AC và \[\widehat {ABC} = \widehat {ACB}\].
Xét ∆ABM và ∆ACN, có:
AB = AC (chứng minh trên).
\[\widehat {ABC} = \widehat {ACB}\] (chứng minh trên).
BM = CN (giả thiết).
Do đó ∆ABM = ∆ACN (cạnh – góc – cạnh).
Suy ra AM = AN (cặp cạnh tương ứng).
Do đó ∆AMN cân tại A.
Vậy ta chọn đáp án A.
Câu 4:
Cho hình bên.
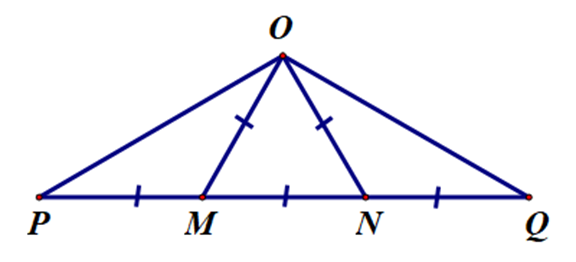
Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát hình, ta thấy OM = ON = MN.
Do đó ∆OMN là tam giác đều.
Quan sát hình, ta thấy OM = PM.
Do đó ∆OPM là tam giác cân tại M.
Quan sát hình, ta thấy ON = NQ.
Do đó ∆ONQ là tam giác cân tại N.
Khi đó ta có: ∆OMN là tam giác đều; ∆OPM và ∆ONQ là các tam giác cân.
Do đó đáp án B, C đều đúng.
Vậy ta chọn đáp án D.
Câu 5:
\[\widehat {xOy} = 120^\circ \]. Lấy điểm A thuộc tia phân giác của \[\widehat {xOy}\]. Kẻ AB ⊥ Ox tại B, AC ⊥ Oy tại C. Hỏi ∆ABC là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
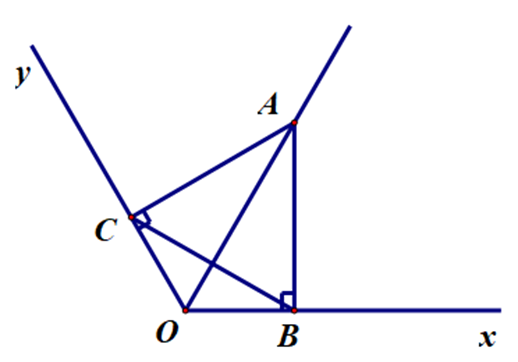
Xét ∆OAB và ∆OAC, có:
\[\widehat {ACO} = \widehat {ABO} = 90^\circ \].
OA là cạnh chung.
\[\widehat {AOC} = \widehat {AOB}\] (OA là phân giác của \[\widehat {xOy}\]).
Do đó ∆OAB = ∆OAC (cạnh huyền – góc nhọn).
Suy ra AB = AC (cặp cạnh tương ứng).
Do đó ∆ABC cân tại A (1).
Ta có OA là phân giác của \[\widehat {xOy}\].
Suy ra \[\widehat {BOA} = \widehat {AOC} = \frac{{120^\circ }}{2} = 60^\circ \].
∆OAB vuông tại B: \[\widehat {BOA} + \widehat {OAB} = 90^\circ \].
Suy ra \[\widehat {OAB} = 90^\circ - \widehat {BOA} = 90^\circ - 60^\circ = 30^\circ \].
Chứng minh tương tự, ta được \[\widehat {OAC} = 30^\circ \].
Do đó ta có \[\widehat {OAB} + \widehat {OAC} = 30^\circ + 30^\circ = 60^\circ \].
Ta suy ra \[\widehat {BAC} = 60^\circ \] (2).
Từ (1), (2), ta suy ra ∆ABC là tam giác đều.
Vậy ta chọn đáp án D.
Câu 6:
Cho ∆ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc canh AB sa cho AD = AE. Gọi I là giao điểm của BD và CE. Hỏi ∆IBC là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
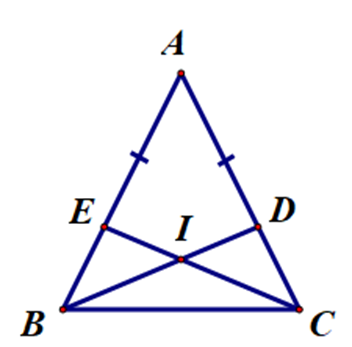
Vì ∆ABC cân tại A nên AB = AC.
Xét ∆ABD và ∆ACE, có:
AB = AC (chứng minh trên).
\[\widehat {BAC}\] là góc chung.
AD = AE (giả thiết).
Do đó ∆ABD = ∆ACE (cạnh – góc – cạnh).
Suy ra \[\widehat {ABD} = \widehat {ACE}\] (cặp cạnh tương ứng).
Vì ∆ABC cân tại A nên \[\widehat {ABC} = \widehat {ACB}\].
Suy ra \[\widehat {ABD} + \widehat {DBC} = \widehat {ACE} + \widehat {ECB}\].
Mà \[\widehat {ABD} = \widehat {ACE}\] (chứng minh trên).
Do đó \[\widehat {DBC} = \widehat {ECB}\] hay \[\widehat {IBC} = \widehat {ICB}\].
Khi đó ta có ∆IBC cân tại I.
Vậy ta chọn đáp án A.
Câu 7:
Cho ∆ABC vuông tại A (AB < AC). Tia phân giác của \[\widehat A\] cắt BC tại D. Qua D kẻ đường thẳng vuông góc BC, cắt AC tại E. Trên AB lấy điểm F sao cho AF = AE. Hỏi ∆DBF là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
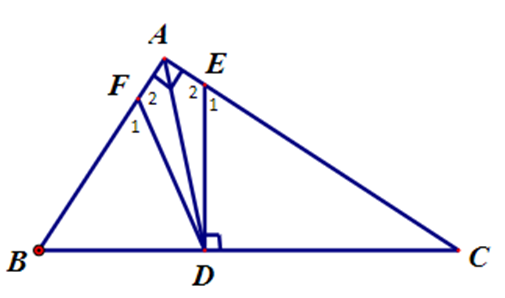
Xét ∆EAD và ∆FAD, có:
AF = AE (giả thiết).
\[\widehat {FAD} = \widehat {DAE}\] (AD là phân giác \[\widehat {BAC}\]).
AD là cạnh chung.
Do đó ∆EAD = ∆FAD (cạnh – góc – cạnh).
Suy ra \[\widehat {{E_2}} = \widehat {{F_2}}\].
Ta có \[\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \] (hai góc kề bù).
Lại có \[\widehat {{F_1}} + \widehat {{F_2}} = 180^\circ \] (hai góc kề bù).
Do đó ta có \[\widehat {{E_1}} = \widehat {{F_1}}\] (1).
∆ABC vuông tại A: \[\widehat {ABC} + \widehat {ACB} = 90^\circ \].
∆CDE vuông tại D: \[\widehat {DEC} + \widehat {ACB} = 90^\circ \].
Do đó \[\widehat {ABC} = \widehat {DEC}\] hay \[\widehat {FBD} = \widehat {{E_1}}\] (2).
Từ (1), (2), ta suy ra \[\widehat {FBD} = \widehat {{F_1}}\].
Do đó ∆FBD cân tại D.
Vậy ta chọn đáp án C.
Câu 8:
Cho hình vẽ.
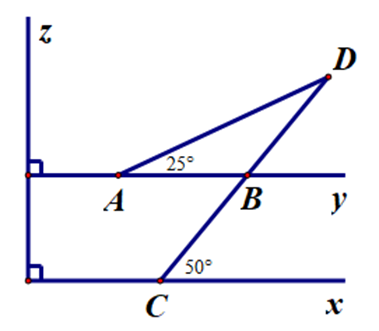
Tam giác cân trong hình vẽ bên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta thấy x ⊥ z và y ⊥ z (giả thiết).
Suy ra x // y.
Có \[\widehat {ABC},\,\,\widehat {BCx}\] ở vị trí so le trong.
Do đó \[\widehat {ABC} = \widehat {BCx} = 50^\circ \].
Ta có \[\widehat {ABC} + \widehat {ABD} = 180^\circ \] (hai góc kề bù).
Suy ra \[\widehat {ABD} = 180^\circ - \widehat {ABC} = 180^\circ - 50^\circ = 130^\circ \].
Xét ∆ABD, có: \[\widehat {ABD} + \widehat {BAD} + \widehat {ADB} = 180^\circ \].
Suy ra \[\widehat {ADB} = 180^\circ - \widehat {ABD} - \widehat {BAD} = 180^\circ - 130^\circ - 25^\circ = 25^\circ \].
Do đó \[\widehat {ADB} = \widehat {BAD}\].
Khi đó ta được ∆ABD cân tại B.
Do đó đáp án B đúng.
Đáp án A sai vì \[\widehat {ADB} = 25^\circ \] nên ∆ACD không phải là tam giác đều.
Đáp án C sai vì ba điểm B, C, D là ba điểm thẳng hàng nên không thể tạo thành một tam giác.
Đáp án D sai vì ta đã chứng minh được hình vẽ có ∆ABD cân tại B.
Vậy ta chọn đáp án B.
Câu 9:
Cho hình vẽ.
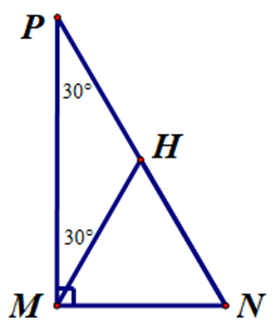
Tam giác đều trong hình vẽ bên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có \[\widehat {PMN} = 90^\circ \] (∆MNP vuông tại M).
Suy ra \[\widehat {PMH} + \widehat {HMN} = 90^\circ \].
Do đó \[\widehat {HMN} = 90^\circ - \widehat {PMH} = 90^\circ - 30^\circ = 60^\circ \] (1).
∆MNP vuông tại M: \[\widehat {MNH} + \widehat {MPH} = 90^\circ \].
Suy ra \[\widehat {MNH} = 90^\circ - \widehat {MPH} = 90^\circ - 30^\circ = 60^\circ \] (2).
Từ (1), (2), ta suy ra ∆MNH là tam giác đều.
Do đó đáp án D đúng.
Đáp án A sai vì ∆MNP là tam giác vuông tại M.
Đáp án B sai vì ba điểm P, N, H là ba điểm thẳng hàng nên không thể tạo thành một tam giác.
Đáp án C sai vì \[\widehat {MPH} = \widehat {PMH} = 30^\circ \] nên ∆MPH cân tại H.
Vậy ta chọn đáp án D.
Câu 10:
Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự các điểm D, E, F sao cho AD = BE = CF. Hỏi ∆DEF là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
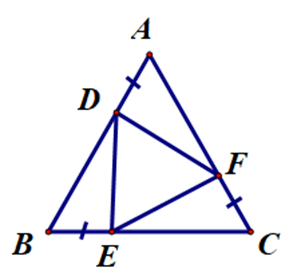
Vì ba điểm A, D, B thẳng hàng nên BD = AB – AD.
Vì ba điểm A, F, C thẳng hàng nên AF = AC – CF.
Ta có AB = AC (∆ABC đều) và AD = CF (giả thiết).
Do đó AB – AD = AC – CF.
Suy ra BD = AF.
Xét ∆ADF và ∆BED, có:
AD = BE (giả thiết).
BD = AF (chứng minh trên).
Do đó ∆ADF = ∆BED (cạnh – góc – cạnh).
Suy ra \[\widehat {FDA} = \widehat {DEB}\] (cặp góc tương ứng).
Xét ∆BDE, có: \[\widehat {BDE} + \widehat {EBD} + \widehat {DEB} = 180^\circ \].
Suy ra \[\widehat {BDE} + 60^\circ + \widehat {FDA} = 180^\circ \] (∆ABC đều).
Mà \[\widehat {BDE} + \widehat {EDF} + \widehat {FDA} = 180^\circ \] (kề bù).
Do đó \[\widehat {EDF} = 60^\circ \].
Chứng minh tương tự, ta được \[\widehat {DEF} = 60^\circ \].
Ta suy ra ∆DEF đều.
Do đó đáp án A đúng.
∆DEF là tam giác đều nên ∆DEF không thể là tam giác vuông (vì tam giác đều có các góc bằng nhau và cùng bằng 60°).
Do đó ta loại đáp án B, C, D.
Vậy ta chọn đáp án A.
