Đề kiểm tra cuối học kì 2 Toán lớp 7 CTST - Đề 01 có đáp án
-
1107 lượt thi
-
21 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Chọn khẳng định sai:
Với điều kiện các tỉ số đều có nghĩa thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có \[\frac{x}{a} = \frac{y}{b} = \frac{z}{c} = \frac{{x + y - z}}{{a + b - c}}\]\[ \ne \frac{{x + y - z}}{{a - b + c}}\] nên D sai.
Câu 2:
Cho biết y tỉ lệ thuận với x theo tỉ số k (k ≠ 0) và x tỉ lệ thuận với z theo tỉ số h (h ≠ 0). Chọn khẳng định đúng trong các khẳng định sau.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì y tỉ lệ thuận với x theo tỉ số k (k ≠ 0) nên ta có y = kx;
x tỉ lệ thuận với z theo tỉ số h (h ≠ 0) nên ta có x = hz.
Khi đó ta có y = kx = k.(hz) = (kh).z nên y và z tỉ lệ thuận với nhau theo hệ số tỉ lệ k.h.
Câu 3:
Biểu thức nào sau đây là biểu thức số?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Biểu thức số là: 2.(32 + 4).
Câu 4:
Mệnh đề “Tổng các lập phương của hai số a và b” được biểu thị bởi
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tổng các lập phương của hai số a và b là a3 + b3.
Câu 5:
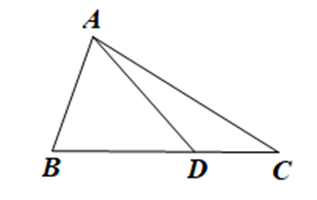
Dựa vào hình vẽ và chọn đáp án đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Nên với tam giác ADC có AD + DC > AC.
Câu 6:
Cho DAMN = DDEK. Đâu là cách kí hiệu bằng nhau khác của hai tam giác trên?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì DAMN = DDEK nên \(\left\{ {\begin{array}{*{20}{c}}{\widehat A = \widehat D\,;\,\,\widehat M = \widehat E\,;\,\,\widehat N = \widehat K}\\{AM = DE\,;\,\,MN = EK\,;\,\,AN = DK}\end{array}} \right.\)
Vậy một trong những cách kí hiệu bằng nhau khác của hai tam giác trên là:
DANM = DDKE.
Câu 7:
Cho tam giác ABC. Ba đường trung tuyến của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ba đường trung tuyến của tam giác ABC cùng đi qua một điểm M, điểm M này gọi là trọng tâm của tam giác ABC.
Câu 8:
Một phép thử nghiệm có n kết quả và tất cả các kết quả đều có khả năng như nhau. Khi đó xác suất xảy ra của mỗi kết quả đều bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Khi tất cả các kết quả của một trò chơi hay phép thử nghiệm ngẫu nhiên đều có khả năng xảy ra bằng nhau thì xác suất xảy ra của mỗi kết quả đều là \[\frac{1}{n}\], trong đó n là số các kết quả.
Câu 9:
Tìm x, biết:
 Xem đáp án
Xem đáp án
\[\frac{{x - 1}}{3} = \frac{1}{2}\]
2.(x – 1) = 3.1
2x – 2 = 3
2x = 5
\(x = \frac{5}{2}\)
Vậy \(x = \frac{5}{2}\).Câu 10:
Tìm x, biết:
5x(x – 3) = (x – 2)(5x – 1) – 5.
 Xem đáp án
Xem đáp án
5x(x – 3) = (x – 2)(5x – 1) – 5
5x2 – 15x = 5x2 – x – 10x + 2 – 5
–4x = –3
\[\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{3}{4}\]
Vậy \(x = \frac{3}{4}\).
Câu 11:
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
 Xem đáp án
Xem đáp án
A(x) = x – 2x2 + 3x5 + x4 + x + x2
= 3x5 + x4 – x2 + 2x.
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5
= – 3x5 – x4 + x2 + x – 2
Câu 12:
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm đa thức M(x) sao cho B(x) = A(x) + M(x). Tìm bậc và hệ số cao nhất của đa thức M(x).
 Xem đáp án
Xem đáp án
B(x) = A(x) + M(x)
Suy ra M(x) = B(x) – A(x)
M(x) = (– 3x5 – x4 + x2 + x – 2) – (3x5 + x4 – x2 + 2x)
= – 3x5 – x4 + x2 + x – 2 – 3x5 – x4 + x2 – 2x
= –6x5 – 2x4 + 2x2 – x – 2.
Đa thức M(x) có bậc là 5, hệ số cao nhất là –6.
Câu 13:
Cho hai đa thức A(x) = x – 2x2 + 3x5 + x4 + x + x2;
B(x) = –2x2 + x – 2 – x4 + 3x2 – 3x5.
Tìm nghiệm của đa thức N(x) biết A(x) = N(x) – B(x).
 Xem đáp án
Xem đáp án
A(x) = N(x) – B(x)
Suy ra N(x) = A(x) + B(x)
N(x) = (3x5 + x4 – x2 + 2x) + (– 3x5 – x4 + x2 + x – 2)
= 3x5 + x4 – x2 + 2x – 3x5 – x4 + x2 + x – 2
= – x – 2.
N(x) = 0
Suy ra – x – 2 nên x = – 2.
Vậy đa thức N(x) có nghiệm là x = – 2.
Câu 14:
Ba phân xưởng in có tổng cộng có 47 máy in (có cùng công suất in) và mỗi phân xưởng được giao in một số trang in bằng nhau. Phân xưởng thứ nhất hoàn thành công việc trong 3 ngày, phân xưởng thứ hai trong 4 ngày và phân cưởng thứ ba trong 5 ngày. Hỏi mỗi phân xưởng có bao nhiêu máy in?
 Xem đáp án
Xem đáp án
Gọi x, y, z lần lượt là số máy in của các phân xưởng thứ nhất, thứ hai, thứ ba.
Tổng số máy của ba phân xưởng là x + y + z = 47.
Vì số ngày hoàn thành công việc tỉ lệ nghịch với số máy nên ta có:
3x = 4y = 5z hay \(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}}\).
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{\frac{1}{3}}} = \frac{y}{{\frac{1}{4}}} = \frac{z}{{\frac{1}{5}}} = \frac{{x + y + z}}{{\frac{1}{3} + \frac{1}{4} + \frac{1}{5}}} = \frac{{47}}{{\frac{{47}}{{60}}}} = 60\)
Suy ra \(x = 60.\frac{1}{3} = 20;\) \(y = 60.\frac{1}{4} = 15;\) \(z = 60.\frac{1}{5} = 12\).
Vậy số máy in của ba phân xưởng lần lượt là 20; 15; 12 (máy in).
Câu 15:
Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Xét các biến cố sau:
A: “Quả bóng lấy ra ghi số nguyên tố”;
B: “Quả bóng lấy ra ghi số chia hết cho 5”;
C: “Quả bóng lấy ra ghi số chia hết cho 6”.
D: “Quả bóng lấy ra ghi số tròn chục”.
Trong các biến cố trên, chỉ ra biến cố nào là chắc chắn, không thể.
 Xem đáp án
Xem đáp án
Biến cố B là biến cố chắc chắn, biến cố C là biến cố không thể.
Câu 16:
Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Xét các biến cố sau:
A: “Quả bóng lấy ra ghi số nguyên tố”;
B: “Quả bóng lấy ra ghi số chia hết cho 5”;
C: “Quả bóng lấy ra ghi số chia hết cho 6”.
D: “Quả bóng lấy ra ghi số tròn chục”.
Tính xác suất của các biến cố A và D.
 Xem đáp án
Xem đáp án
Vì 5 quả bóng có kích thước và khối lượng như nhau nên mỗi quả bóng đều có cùng khả năng được chọn.
• Trong 5 quả bóng ghi lần lượt các số 5; 10; 15; 20; 25, chỉ có 1 quả bóng ghi số nguyên tố là 5. Do đó xác xuất của biến cố A là \(P\left( A \right) = \frac{1}{5}\).
• Trong 5 quả bóng ghi lần lượt các số 5; 10; 15; 20; 25, có 2 quả bóng ghi số tròn chục là 10; 20. Do đó xác xuất của biến cố D là \(P\left( A \right) = \frac{2}{5}\).
Câu 17:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
So sánh các góc của tam giác ABC.
 Xem đáp án
Xem đáp án

Tam giác ABC là tam giác vuông tại A nên cạnh huyền BC là cạnh lớn nhất.
Mà AB < AC nên AB < AC < BC.
Suy ra \(\widehat C < \widehat B < \widehat A\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Câu 18:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Chứng minh DABM = DDBM. Từ đó suy ra MA = MD.
 Xem đáp án
Xem đáp án
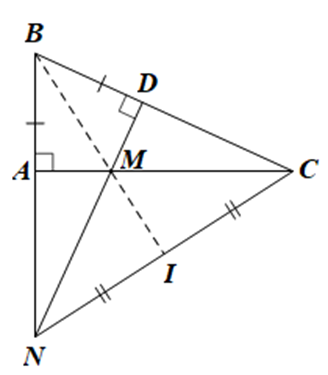
Xét DABM và DDBM có:
\(\widehat {BAM} = \widehat {BDM} = 90^\circ \);
BA = BD (giả thiết);
BM là cạnh chung
Do đó DABM = DDBM (cạnh huyền – cạnh góc vuông)
Suy ra MA = MD (hai cạnh tương ứng).
Câu 19:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Tam giác MNC là tam giác gì? Tại sao?
 Xem đáp án
Xem đáp án

Xét DANM và DDCM có:
\(\widehat {NAM} = \widehat {CDM} = 90^\circ \);
MA = MD (chứng minh câu b);
\(\widehat {AMN} = \widehat {DMC}\) (hai góc đối đỉnh).
Do đó DANM = DDCM (cạnh góc vuông – góc nhọn kề)
Suy ra MN = MC (hai cạnh tương ứng).
Tam giác MNC có MN = MC nên là tam giác cân tại M.
Câu 20:
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm D sao cho BD = BA. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.
 Xem đáp án
Xem đáp án
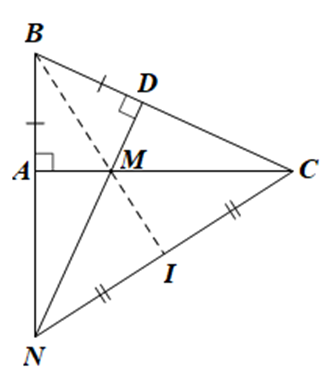
Do DMNC cân tại M có I là trung điểm của NC nên MI là đường trung tuyến của DMNC.
Khi đó MI đồng thời là đường cao của DMNC hay MI ⊥ NC (1)
Xét DBNC có hai đường cao CA, ND cắt nhau tại M nên M là trực tâm của DBNC.
Suy ra BM ⊥ NC (2)
Từ (1) và (2) suy ra ba điểm B, M, I thẳng hàng.
Câu 21:
Tìm giá trị nguyên dương của x để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
 Xem đáp án
Xem đáp án
Thực hiện phép chia đa thức như sau:
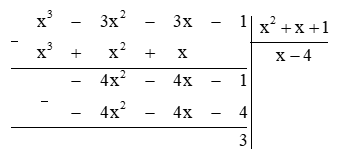
Để đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1 thì 3 ⋮ (x2 + x + 1).
Tức là x2 + x + 1 ∈ Ư(3) = {–3; 3; –1; 1}.
Do x > 0 nên x2 + x + 1 > 1
Do đó x2 + x + 1 = 3
x2 + x – 2 = 0
x2 – x + 2x – 2 = 0
x(x – 1) + 2(x – 1) = 0
(x – 1)(x + 2) = 0
Suy ra x = 1 (thỏa mãn) hoặc x = – 2 (loại).
Vậy x = 1 thì đa thức x3 – 3x2 – 3x – 1 chia hết cho đa thức x2 + x + 1.
