Đề thi Học kì 1 Toán 7 CTST có đáp án (Đề 1)
-
1293 lượt thi
-
18 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trong các số sau, số nào biểu diễn số hữu tỉ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì −2; 9 ∈ ℤ; 9 ≠ 0 nên Î ℚ hay 12,5 ∈ ℚ.
Do đó số biểu diễn số hữu tỉ.
Chọn đáp án A.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số là số vô tỉ.
Do đó thuộc tập hợp 𝕀.
Câu 5:
Cho điểm M nằm ngoài đường thẳng d. Có bao nhiêu đường thẳng qua M và song song với d?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo tiên đề Euclid: Qua một điểm nằm ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Do đó, với điểm M nằm ngoài đường thẳng d, có duy nhất một đường thẳng qua M và song song với d.
Chọn đáp án B.
Câu 6:
Trong các kết quả sau, kết quả nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
∙ Kết quả là sai vì .
∙ Kết quả là sai vì (căn bậc hai số học của một số là một số nguyên không âm).
∙ Kết quả là sai vì số âm không có căn bậc hai số học.
∙ Kết quả là đúng.
Câu 7:
Cho lăng trụ đứng có kích thước như hình vẽ.
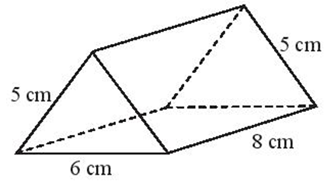
Số nào trong các số sau đây là diện tích xung quanh của hình lăng trụ đứng đó?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
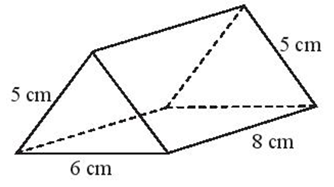
Hình vẽ trên là hình lăng trụ đứng tam giác.
Chu vi đáy hình tam giác là:
5 + 5 + 6 = 16 (cm)
Diện tích xung quanh của hình lăng trụ đứng là:
16 . 8 = 128 (cm2)
Vậy diện tích xung quanh của hình lăng trụ đứng là 128 cm2.
Câu 8:
Cho hình vẽ sau:
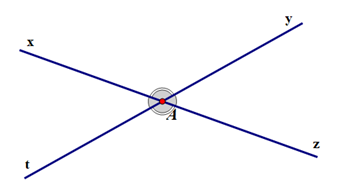
Góc đối đỉnh với góc xAy là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
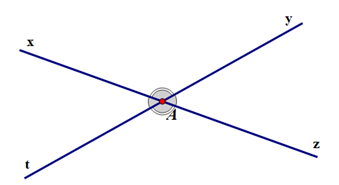
Trong hình vẽ trên, ta thấy:
- Cạnh Ax của góc xAy là tia đối của cạnh Az của góc tAz;
- Cạnh Ay của góc xAy là tia đối của cạnh At của góc tAz.
Do đó, góc đối đỉnh với góc xAy là góc tAz.
Chọn đáp án C.
Câu 9:
Trong các câu sau, câu nào cho một định lí?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Câu 10:
Hình lập phương A có cạnh bằng cạnh hình lập phương B. Hỏi thể tích hình lập phương A bằng bao nhiêu phần thể tích hình lập phương B?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi cạnh hình lập phương A là a.
Cạnh hình lập phương B là .
Thể tích hình lập phương A là a3.
Thể tích hình lập phương A là .
Thể tích hình lập phương A bằng số phần thể tích hình lập phương B là:
.
Vậy thể tích hình lập phương A bằng thể tích hình lập phương B.
Câu 11:
Biểu đồ dưới đây cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả ở một trang trại.
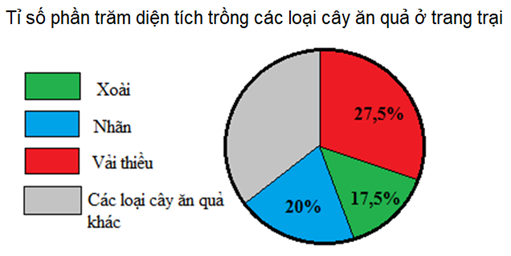
Căn cứ vào biểu đồ sau đây, hãy cho biết tỉ số phần trăm diện tích trồng các loại cây ăn quả khác là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào biểu đồ, ta thấy:
- Tỉ số phần trăm diện tích trồng cây xoài là 17,5%;
- Tỉ số phần trăm diện tích trồng cây nhãn là 20%;
- Tỉ số phần trăm diện tích trồng cây vải thiều là 27,5%.
Do đó, tỉ số phần trăm diện tích trồng các loại cây ăn quả khác là:
100% − 17,5% − 20% − 27,5% = 35%.
Vậy tỉ số phần trăm diện tích trồng các loại cây ăn quả khác là 35%.
Câu 12:
Cho biểu đồ sau:
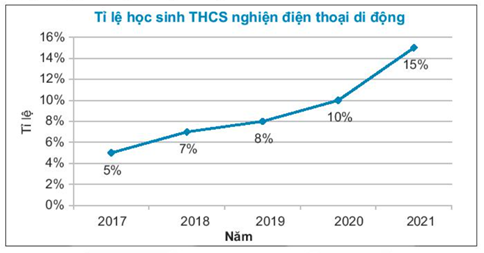
Năm nào có tỉ lệ học sinh THCS nghiện điện thoại cao nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tỉ lệ học sinh THCS nghiện điện thoại của năm 2017, năm 2018, năm 2019, năm 2020 và năm 2021 lần lượt là 5%, 7%, 8%, 10%, 15%.
Ta thấy: 5% < 7% < 8% < 10% < 15%.
Suy ra tỉ lệ học sinh THCS nghiện điện thoại là 15%.
Vậy tỉ lệ học sinh THCS nghiện điện thoại cao nhất là năm 2021.
Câu 13:
 Xem đáp án
Xem đáp án
Chiều cao của mực nước ở trong bể là:
1,2 - 0,4 = 0,8 (m)
Thể tích nước trong bể cá với chiều dài 2 m, chiều rộng 1,5 m và chiều cao 0,8 m là
2 . 1,5 . 0,8 = 2,4 (m3).
Vậy thể tích nước trong bể cá là 2,4 m3.
Câu 14:
 Xem đáp án
Xem đáp án
Gọi bán kính hình tròn là R (cm).
Diện tích của hình tròn là: πR2 = 300 (cm2).
Bán kính của hình tròn là: (cm).
Vậy bán kính của hình tròn khoảng bằng 9,77 cm.
Câu 15:
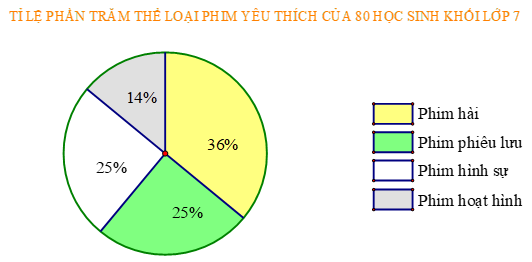
a) Trong biểu đồ trên, có mấy thể loại phim đươc được thống kê.
 Xem đáp án
Xem đáp án
a) Trong biểu đồ trên, có 4 thể loại phim đươc được thống kê gồm: Phim hài, phim phiêu lưu, phim hình sự, phim hoạt hình.
Câu 16:
b) Loại phim nào được các bạn học sinh khối lớp 7 yêu thích nhất?
 Xem đáp án
Xem đáp án
b) Tỉ số phần trăm các loại thể loại phim:
- Phim hài chiếm 36%;
- Phim phiêu lưu chiếm 25%;
- Phim hình sự chiếm 25%;
- Phim hoạt hình chiếm 14%.
Do đó, tỉ lệ phần trăm lớn nhất là 36%.
Vậy phim hài được các bạn học sinh khối lớp 7 yêu thích nhất.
Câu 17:
Cho tam giác ABC có , tia phân giác góc C cắt AB tại D. Tính .
 Xem đáp án
Xem đáp án
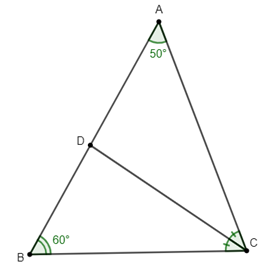
Xét tam giác ABC có:
(định lý tổng ba góc trong tam giác).
Suy ra
Do đó .
Vì CD là tia phân giác của góc C nên:
Xét tam giác ABC có:
(định lý tổng ba góc trong tam giác).
Suy ra .
Do đó .
Vì và là hai góc kề bù nên .
.
Vậy .
Câu 18:
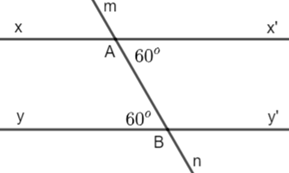
Vẽ lại hình bên và giải thích tại sao xx' // yy'.
 Xem đáp án
Xem đáp án
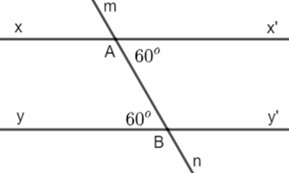
Trong hình vẽ trên, ta thấy:
Mà và ở vị trí đồng vị.
Do đó xx' // yy'.
