Trắc nghiệm Toán 7 Bài 3. Hai đường thẳng song song có đáp án
-
457 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
Xem đáp án
Đáp án đúng là: A
Theo tiên đề Euclid ta có: qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Câu 2:
Nếu một đường thẳng cắt hai đường thẳng song song thì:
Xem đáp án
Đáp án đúng là: A
Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc đồng vị bằng nhau;
Hai góc so le trong bằng nhau.
Câu 3:
Cho hình vẽ dưới đây:
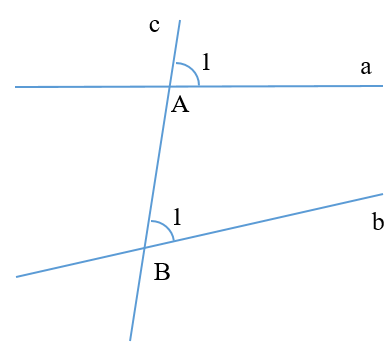
\[\widehat {{A_1}}\] và \[\widehat {{B_1}}\] là hai góc:
A. so le trong;
Xem đáp án
Đáp án đúng là: C
\[\widehat {{A_1}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị.
Câu 4:
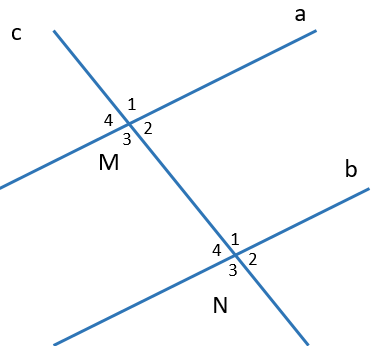
Chọn phát biểu đúng.
Xem đáp án
Đáp án đúng là: D
\[\widehat {{M_1}}\] và \[\widehat {{N_1}}\] là hai góc so le trong là phát biểu sai, vì đó là hai góc đồng vị, loại phương án A;
\[\widehat {{M_2}}\] và \[\widehat {{N_2}}\] là hai góc so le ngoài là phát biểu sai, vì đó là hai góc đồng vị, loại phương án B;
\[\widehat {{M_3}}\] và \[\widehat {{N_1}}\] là hai góc đồng vị là phát biểu sai, vì đó là hai góc so le trong, loại phương án C;
\[\widehat {{M_4}}\] và \[\widehat {{N_4}}\] là hai góc đồng vị là phát biểu đúng, chọn phương án D.
Câu 5:
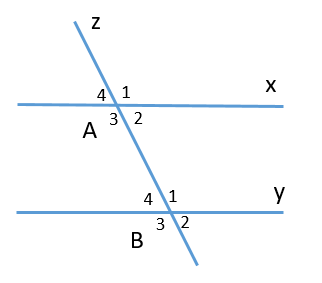
Chọn một cặp góc đồng vị trong hình vẽ sau:
Xem đáp án
Đáp án đúng là: B
\[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc kề bù, loại phương án A.
\[\widehat {{B_2}}\] và \[\widehat {{B_3}}\] là hai góc đồng vị là phát biểu đúng, chọn phương án B.
\[\widehat {{A_2}}\] và \[\widehat {{B_4}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{A_2}}\] và \[\widehat {{B_4}}\] là hai góc so le trong, loại phương án C.
\[\widehat {{A_4}}\] và \[\widehat {{A_2}}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {{A_4}}\] và \[\widehat {{A_2}}\] là hai góc đối đỉnh, loại phương án D.
Câu 6:
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
Xem đáp án
Đáp án đúng là: A
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì x, y song song với nhau.
Câu 7:
Cho hình vẽ
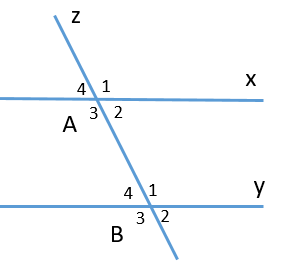
Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 30^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].
Xem đáp án
Đáp án đúng là: D
Ta có:
\[\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \] (hai góc kề bù)
\[ \Rightarrow \widehat {{B_3}} = 180^\circ - 30^\circ = 150^\circ \]
\[ \Rightarrow \widehat {{A_3}}\; = \widehat {{B_3}} = 150^\circ \]
=> Chọn phương án D.
Câu 8:
Biết một cặp góc so le trong \[\widehat {{A_2}}\; = \widehat {{B_4}} = 36^\circ \]. Tính số đo của cặp góc so le trong còn lại:
Xem đáp án
Đáp án đúng là: A
Ta có:
\[\widehat {{A_2}} + \widehat {{A_3}} = 180^\circ \] (hai góc kề bù)
\[ \Rightarrow \widehat {{A_3}} = 180^\circ - {36^o} = 144^\circ \]
Mà \[\widehat {{A_2}}\] và \[\widehat {{B_4}}\]; \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai cặp góc so le trong.
Do đó, \[\widehat {{A_3}} = \widehat {{B_1}} = 144^\circ \]
Vậy số đo của cặp góc so le trong còn lại là \[\widehat {{A_3}} = \widehat {{B_1}} = 144^\circ \].
Câu 9:
Cho hình vẽ
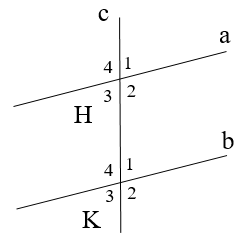
Biết \[\widehat {{K_1}} = \widehat {{H_3}} = 42^\circ .\]. Tính \[\widehat {{H_3}} + \widehat {{K_4}}\]
Xem đáp án
Đáp án đúng là: A
Xét hai đường thẳng a và b cùng cắt đường thẳng c có: \[\widehat {{K_1}} = \widehat {{H_3}}\]
Mà hai góc này ở vị trí so le trong nên a // b
Suy ra \(\widehat {{H_3}} + \widehat {{K_4}} = 180^\circ \) (hai góc ở vị trí trong cùng phía)
Vậy \(\widehat {{H_3}} + \widehat {{K_4}} = 180^\circ \)
Câu 10:
Cho hình vẽ
Biết a // b, \[\widehat {{H_3}} = 42^\circ \]. Tính số đo \[\widehat {{K_3}}\]
Xem đáp án
Đáp án đúng là: C
Vì a // b nên \(\widehat {{H_3}} = \widehat {{K_3}}\) ( do \[\widehat {{H_3}}\] và \[\widehat {{K_3}}\] là hai góc đồng vị).
Suy ra \[\widehat {{K_3}} = 42^\circ \].
Vậy \[\widehat {{K_3}} = 42^\circ \].
Câu 11:
Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
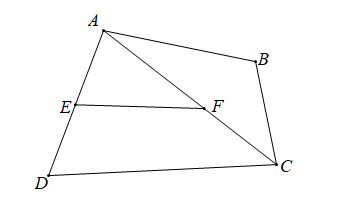
Xem đáp án
Đáp án đúng là: B
\[\widehat {DAC}\] và \[\widehat {AFE}\] là hai góc so le trong là phát biểu sai, vì \[\widehat {DAC}\] và \[\widehat {AFE}\] là hai góc trong một tam giác loại phương án A.
\[\widehat {AFE}\] và \[\widehat {BAC}\] là hai góc so le trong là phát biểu đúng, chọn phương án B.
\[\widehat {AFE}\] và \[\widehat {ADC}\] là hai góc đồng vị là phát biểu sai.
\[\widehat {BAC}\] và \[\widehat {DAC}\] là hai góc đồng vị là phát biểu sai, vì \[\widehat {BAC}\] và \[\widehat {DAC}\] có đỉnh chung và có một cạnh chung nên là hai góc kề nhau, do đó loại phương án D.
Câu 12:
Cho hình vẽ
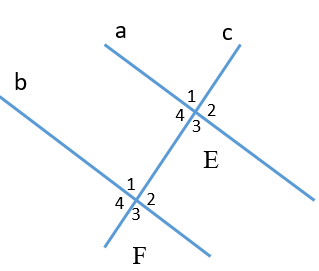
Biết a // b,
\[{\widehat E_1} = 51^\circ \]. Số đo \[\widehat {{F_3}}\] là:
Xem đáp án
Đáp án đúng là: A.
Ta có: \[\widehat {{E_1}}\] và \[\widehat {{F_1}}\] là hai góc đồng vị và a // b => \[\widehat {{E_1}} = \widehat {{F_1}} = 51^\circ \]
Mà ta lại có \[\widehat {{F_1}}\] và \[\widehat {{F_3}}\] là hai góc đối đỉnh nên => \[\widehat {{F_1}} = \widehat {{F_3}}\]
\[ \Rightarrow \widehat {{F_3}} = 51^\circ \]
Vậy \[\widehat {{F_3}} = 51^\circ .\]
Câu 13:
Trong các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
Xem đáp án
Đáp án đúng là: C
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
Hai góc bù nhau là hai góc có tổng số đo bằng 180o
=> Có 2 câu đúng, chọn đáp án C.
Câu 14:
Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
Xem đáp án
Đáp án đúng là: D
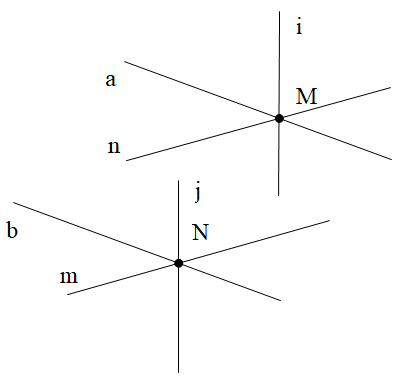
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N (theo Tiên đề Euclid) và song song với đường thẳng đó. Trên hình vẽ ta có b //a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Câu 15:
Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:
Xem đáp án
Đáp án đúng là: A
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
Do đó, qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì hai đường thẳng đó phải trùng nhau.
=> Chọn đáp án A.