Cho tam giác IMN. Trên MN lấy E (IE không vuông góc với MN). Kẻ MP, NQ vuông góc IE. Cho các khẳng định sau:
(I) MP > ME.
(II) MN > MP + NQ.
(III) EN > NQ.
(IV) IQ < IN.
(V) IM < MP.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
A. 1;
B. 2;
C. 3;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
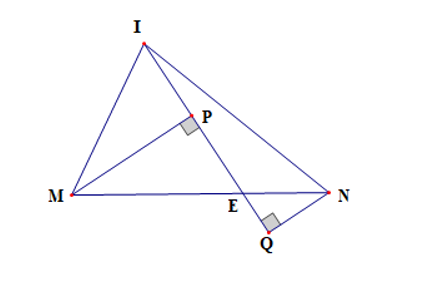
⦁ Ta có MP là đường vuông góc, MI và ME là các đường xiên kẻ từ M đến IQ nên MP < MI, MP < ME.
Do đó khẳng định (I) và (V) là sai.
⦁ Ta có IQ là đường vuông góc, IN là đường xiên kẻ từ I đến NQ nên IQ < IN.
Do đó khẳng định (IV) là đúng.
⦁ Ta có NQ là đường vuông góc, NE là đường xiên kẻ từ N đến EQ nên NQ < NE
Do đó khẳng định (III) là đúng.
⦁ Ta có: MN = ME + EN
Mà MP < ME, NQ < NE
Suy ra MP + NQ < ME + EN = MN.
Do đó khẳng định (II) là đúng.
Vậy có 3 khẳng định đúng, ta chọn phương án C.
Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC. So sánh BC và tổng DH + DK ta được
Hình bên dưới mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM
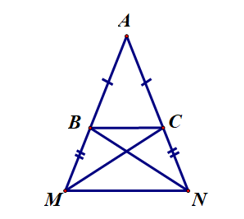
Biết BC = 0,6 m, MN = 0,9 m. Độ dài thanh gỗ BN cần dài ít nhất bao nhiêu là hợp lí?
Cho tam giác ABC cân tại A. Đường cao AH. Lấy điểm M tùy ý trên cạnh BC. Độ dài AM nhỏ nhất khi
Cho hình vẽ dưới đây
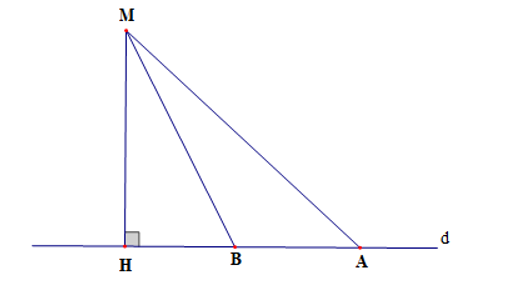
Đoạn thẳng nào có độ dài ngắn nhất trong các đoạn thẳng MH, MB, MA?
Bạn Hoa tập chạy theo các tuyến đường AB, AC, AD, AE, AF như hình vẽ:
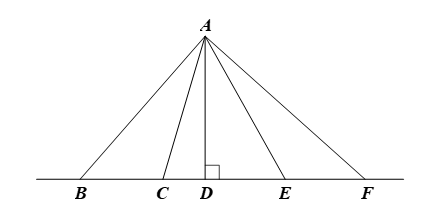
Biết với cùng vận tốc như nhau, Hoa chạy đoạn đường AB mất 15 phút, chạy đoạn AF mất 20 phút. Nếu Hoa chạy đoạn đường AD thì khoảng thời gian nào sau đây là hợp lí nhất?
Cho tam giác ABC đường cao AH, BK. Khẳng định nào sau đây là đúng?
Cho tam giác MNE vuông tại E, A là trung điểm của EM. Gọi H, K lần lượt là hình chiếu của E, M trên AN. Khẳng định nào sau đây là đúng?