Tam giác ABC nội tiếp (O), AD là đường kính của (O). M là trung điểm của của BC, H là trực tâm của tam giác ABC. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC. Chứng minh rằng 4 điểm X, Y, Z, M cùng thuộc 1 đường tròn.
Giải bởi Vietjack
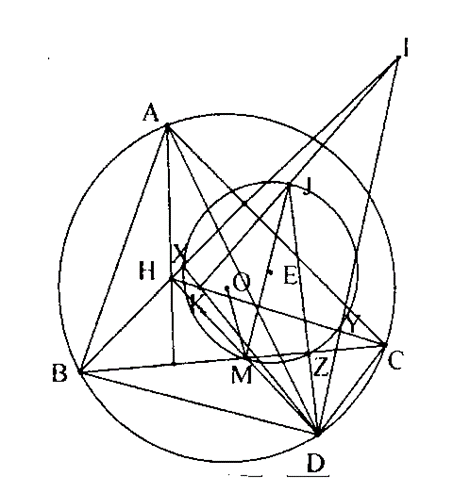
Giả sử HB cắt DY tại I, HC cắt DX tại K, J là trung điểm IK
Xét tam giác ADC có \(\widehat {ACD} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AC ⊥ CD
Mà BH ⊥ AC. Nên BH // CD
Tương tự: \(\widehat {ABD} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
Nên AB ⊥ BD
Mà CH ⊥ AB nên CH // BD
Xét tứ giác BHCD có: BH // CD và CH // BD nên BHCD là hình bình hành.
⇒ HD, BC cắt nhau tại trung điểm M của mỗi đường
Vì DX ⊥ HI, DI ⊥ HC suy ra K là trực tâm của tam giác IHD
Nên: \[\widehat {KDI} = \widehat {KHI} = \widehat {HCD}\](HI //CD)
\(\widehat {CHD} = \widehat {KID}\)(cùng phụ với \(\widehat {HDI}\))
Xét tam giác KID và tam giác CHD có:
\(\widehat {KID} = \widehat {CHD}\)
\[\widehat {KDI} = \widehat {HCD}\]
⇒ ∆KID ∽ ∆CHD (g.g)
Mặt khác CM, DJ là hai trung tuyến tương ứng của tam giác CHD và KID
Như vậy ta có: ∆DIJ ∽ ∆CHM
⇒ \[\widehat {JDI} = \widehat {HCM}\]
Từ đó suy ra: DJ vuông góc với BC tại Z hay Z thuộc đường tròn đường kính MJ.
Lại có: M là trung điểm HD (chứng minh trên)
X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC
Kết hợp tính chất điểm M thì đường tròn đường kính MJ là đường trò Ơ–le của tam giác HID.
Suy ra: X, Y, Z, M cùng thuộc 1 đường tròn.
Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y = (m + 2)x + 2m2 + 1 tìm m để hai đường thẳng (d): y = (m + 2)x + 2m2 + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.
Xem hình vẽ, cho biết a// b và c ⊥ a.
a) Đường thẳng c có vuông góc với đường thẳng b không? Vì sao?
b) Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết \(\widehat {{A_1}} = 115^\circ \). Tính số đo các góc \(\widehat {{B_2}};\widehat {{B_3}};\widehat {{A_3}}\).
c) Gọi Ax và By lần lượt là tia phân giác của các góc \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\). Chứng minh: Ax //By.
người cùng làm một công việc. Nếu làm riêng, người thứ nhất mất 5 giờ, người thứ hai mất 4 giờ và người thứ ba mất 6 giờ mới làm xong công việc đó. Hỏi nếu ba người cùng làm thì sau 1 giờ làm được bao nhiêu phần công việc.
Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?
Cho hình thoi EGHK với O là giao điểm của 2 đường chéo. Biết EG = 15 cm. Tính độ dài của GH, HK, KE?
Chứng minh rằng biểu thức sau luôn dương với mọi x.
a) 9x2 – 6x + 2;
b) x2 + x + 1;
c) 2x2 + 2x + 1.
Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?
Cho hình bình hành ABCD và O là giao điểm của AC và BD. Trên đường chéo AC lấy 2 điểm M và N sao cho AM = MN = NC
a) Chứng minh: tứ giác BMDN là hình bình hành.
b) BC cắt DN tại K. Chứng minh: N là trọng tâm của tam giác BDC.
Cho phương trình x2 + 2(m – 2)x + m2 – 4m = 0.
a) Giải phương trình khi m = 1.
b) Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
Tìm các chữ số a, b để:
a) A = \(\overline {56a3b} \) chia hết cho 18;
b) B = \(\overline {71a1b} \) chia hết cho 45;
c) C = \(\overline {6a14b} \) chia hết cho 2; 3; 5; 9;
d) D = \(\overline {25a1b} \) chia hết cho 15 nhưng không chia hết cho 2.
An có 90 bút bi và 150 quyển vở muốn chia thành các phần thưởng để ủng hộ học sinh nghèo, sao cho số bút và vở trong các phần thưởng là như nhau. Hỏi An chia được bao nhiêu số phần thưởng trong khoảng từ 5 đến 30 phần thưởng?
Viết số có hai chữ số mà chữ số hàng chục bé hơn chữ số hàng đơn vị là 4.
Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài BC. Tính góc B và góc C.
