Cho hình thoi ABCD, O là giao điểm hai đường chéo. Vẽ đường thẳng qua B song song AC, vẽ đường thẳng qua C song song với BD, hai đường thẳng đó cắt nhau tại K.
a) Tứ giác OBKC là hình gì? Vì sao?
b) Chứng minh: AB = OK.
c) Tìm điều kiện của tứ giác ABCD để tứ giác OBKC là hình vuông.
 Giải bởi Vietjack
Giải bởi Vietjack
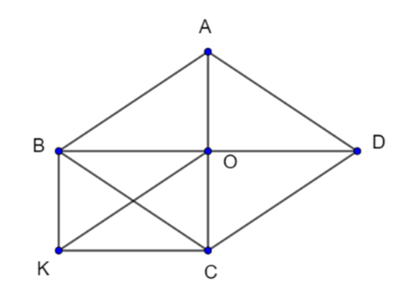
a) Xét hình thoi ABCD có AC và BD là hai đường chéo
Suy ra: AC vuông góc BD tại O ⇒
Ta có:
Tứ giác BOCK có:
Nên ONKC là hình chữ nhật.
b) Vì OBKC là hình chữ nhật (chứng minh câu a)
Nên BC = OK
Mà BC = AB (vì ABCD là hình thoi)
Suy ra AB = OK
Vậy AB = OK
c) OBKC là hình chữ nhật, do đó để OBKC là hình vuông thì OB = OC.
ABCD là hình thoi nên O là trung điểm của AC và BD.
⇒
Mà OB = OC nên AC = BD.
Do đó ABCD là hình vuông.
Vậy ABCD là hình vuông thì tứ giác OBKC là hình vuông.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).
Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N.
a) Chứng minh rằng: DM = EN.
b) MN cắt BC tại I. Chứng minh I là trung điểm của MN.
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.
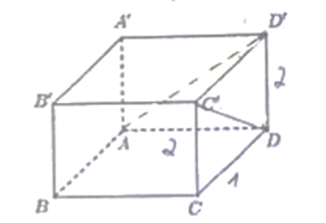
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, BC = 2, AA' = 2. Khoảng cách giữa hai đường thẳng AD' và DC' bằng? (tham khảo hình)
Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Dựng đường tròn (K) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm F, E. Gọi H là giao điểm của BE và CF.
a) Chứng minh rằng AF.AB = AE.AC và AH vuông góc BC.
b) Chứng minh OA vuông góc EF.
Cho hình thoi ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh MNPQ là hình chữ nhật.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.
Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, SA = SB = SC = AC = a, SB tạo với mặt phẳng (SAC) một góc 30°. Tính thể tích khối chóp.
Cho hình thang cân ABCD (AB // CD, AB < CD), BC = 15cm, đường cao BH = 12cm, DH = 16cm. Chứng minh BD vuông góc với BC.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.
a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).
b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.
Cho tam giác ABC có A(1;3), B(-1;-5), C(-4;-1). Viết phương trình đường cao AH của tam giác ABC.
Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, ta vẽ đường thẳng vuông góc với BC, cắt các cạnh AB, AC lần lượt tại E, F. Vẽ các hình chữ nhật BDEH, CDFK. Chứng minh rằng A là trung tâm điểm của HK.