Cho hàm số ![]() .
.
a) Hàm số đã cho đồng biến trên mỗi khoảng ![]() và
và ![]() .
.
b) Giá trị cực đại của hàm số đã cho là ![]() .
.
c) Đồ thị hàm số đã cho đi qua các điểm ![]() .
.
d) Đường thẳng ![]() cắt đồ thị hàm số đã cho tại 3 điểm phân biệt.
cắt đồ thị hàm số đã cho tại 3 điểm phân biệt.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Đ, b) S, c) S, d) S.
Hướng dẫn giải
– Tập xác định của hàm số là ![]() .
.
– Ta có ![]() ;
; ![]() khi
khi ![]() hoặc
hoặc ![]() .
.
Bảng biến thiên của hàm số như sau:
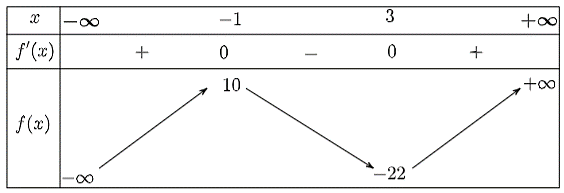
– Hàm số đồng biến trên mỗi khoảng ![]() và
và ![]() ; nghịch biến trên khoảng
; nghịch biến trên khoảng ![]() . Do đó, ý a) đúng.
. Do đó, ý a) đúng.
– Hàm số đã cho đạt cực tiểu tại ![]() ,
, ![]() ; đạt cực đại tại
; đạt cực đại tại ![]() . Do đó, ý b) sai.
. Do đó, ý b) sai.
– Với ![]() thì
thì ![]() ; với
; với ![]() thì
thì ![]() ; với
; với ![]() thì
thì ![]() .
.
Do đó, đồ thị hàm số đã cho đi qua các điểm ![]() .
.
Do đó, ý c) sai.
– Từ bảng biến thiên ta suy ra đường thẳng ![]() cắt đồ thị hàm số đã cho tại 2 điểm phân biệt. Do đó, ý d) sai.
cắt đồ thị hàm số đã cho tại 2 điểm phân biệt. Do đó, ý d) sai.
Cho hàm số ![]() xác định và liên tục trên
xác định và liên tục trên ![]() và có bảng xét dấu như sau:
và có bảng xét dấu như sau:

Hàm số đã cho đạt cực đại tại điểm
Cho hàm số ![]() có đồ thị như hình dưới đây.
có đồ thị như hình dưới đây.

Tâm đối xứng của đồ thị hàm số có tọa độ là
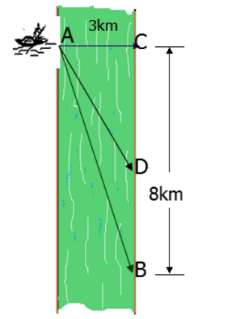
Một người đàn ông muốn chèo thuyền ở vị trí ![]() tới điểm
tới điểm ![]() về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến
về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến ![]() và sau đó chạy đến
và sau đó chạy đến ![]() , hay có thể chèo trực tiếp đến
, hay có thể chèo trực tiếp đến ![]() , hoặc anh ta có thể chèo thuyền đến một điểm
, hoặc anh ta có thể chèo thuyền đến một điểm ![]() giữa
giữa ![]() và
và ![]() và sau đó chạy đến
và sau đó chạy đến ![]() . Biết anh ấy có thể chèo thuyền 6 km/h, chạy 8 km/h và quãng đường
. Biết anh ấy có thể chèo thuyền 6 km/h, chạy 8 km/h và quãng đường ![]() km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Khoảng thời gian ngắn nhất để người đàn ông đến
km. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Khoảng thời gian ngắn nhất để người đàn ông đến ![]() là bao nhiêu giờ (làm tròn kết quả đến hàng phần mười)?
là bao nhiêu giờ (làm tròn kết quả đến hàng phần mười)?
Cho một tấm nhôm hình vuông cạnh 12 cm, người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ![]() (cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
(cm), rồi gập tấm nhôm lại để được một cái hộp có dạng hình hộp chữ nhật không có nắp (tham khảo hình vẽ).
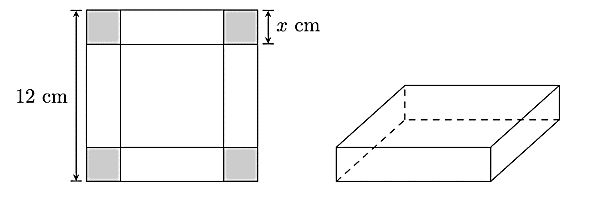
Giá trị của ![]() bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
bằng bao nhiêu centimét để thể tích của khối hộp đó là lớn nhất?
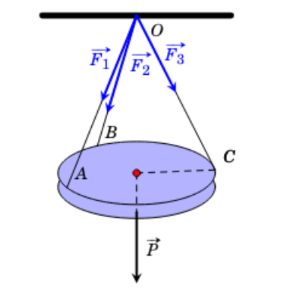
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm ![]() trên trần nhà và lần lượt buộc vào ba điểm
trên trần nhà và lần lượt buộc vào ba điểm ![]() trên đèn tròn sao cho các lực căng
trên đèn tròn sao cho các lực căng ![]() lần lượt trên mối dây
lần lượt trên mối dây ![]() đôi một vuông góc với nhau và
đôi một vuông góc với nhau và ![]() (N) (như hình vẽ). Trọng lượng của chiếc đèn tròn đó là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị)?
(N) (như hình vẽ). Trọng lượng của chiếc đèn tròn đó là bao nhiêu Newton (làm tròn kết quả đến hàng đơn vị)?
Cho hàm số 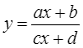 có đồ thị như hình vẽ dưới đây.
có đồ thị như hình vẽ dưới đây.
Khẳng định nào sau đây là đúng?
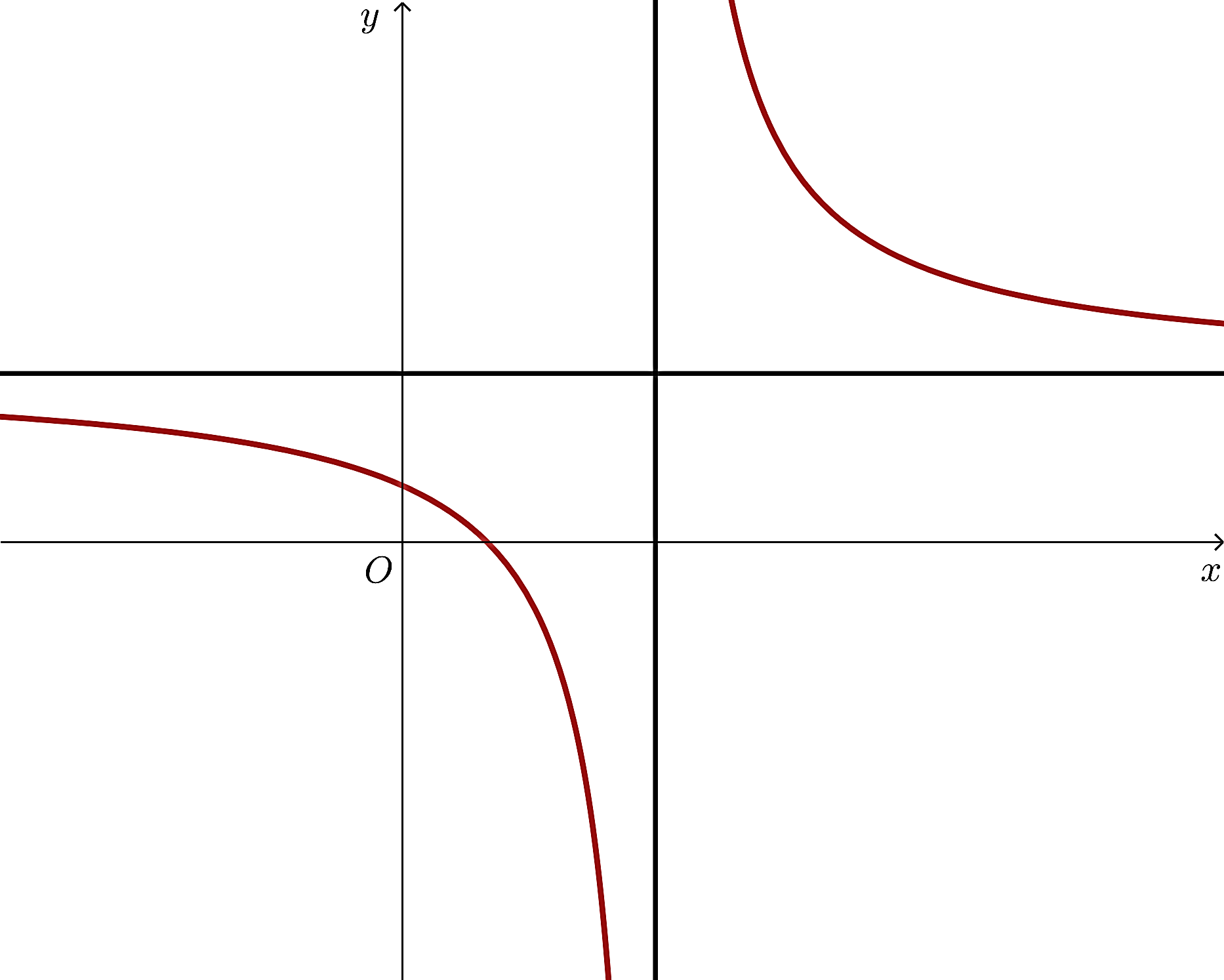
Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành tâm
là hình bình hành tâm ![]() .
. ![]() là điểm thỏa mãn
là điểm thỏa mãn ![]() . Khi đó:
. Khi đó:
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) ![]() .
.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
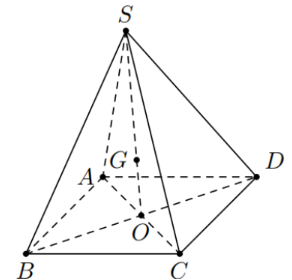
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị như sau:
và có đồ thị như sau:
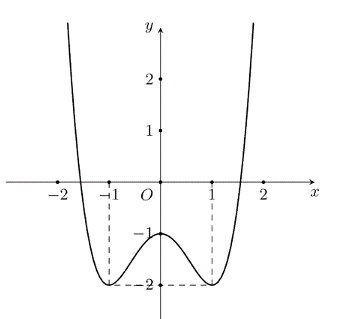
Phát biểu nào dưới đây là đúng?
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
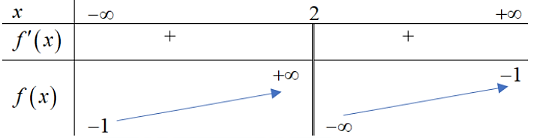
Đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số đã cho lần lượt là:
Cho hình lập phương ![]() có cạnh bằng
có cạnh bằng ![]() . Khi đó:
. Khi đó:
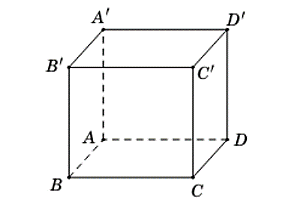
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) Với ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() thì
thì 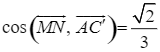 .
.