III. Vận dụng
Một vật chuyển động theo quy luật \(s = - \frac{1}{2}{t^{\rm{3}}}{\rm{ + 9}}{t^{\rm{2}}},\) với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ?
A. 216 (m/s).
B. 30 (m/s).
C. 400 (m/s).
D. 54 (m/s).
Giải bởi Vietjack
Đáp án đúng là: D
Vận tốc chuyển động của vật: \(v(t) = s'(t) = - \frac{3}{2}{t^2} + 18t\) .
Xét hàm \(v(t) = - \frac{3}{2}{t^2} + 18t\) với \(t \in (0;10)\). Ta có \(v'(t) = - 3t + 18;\,\,\,v'(t) = 0 \Leftrightarrow t = 6.\)
Bảng biến thiên:
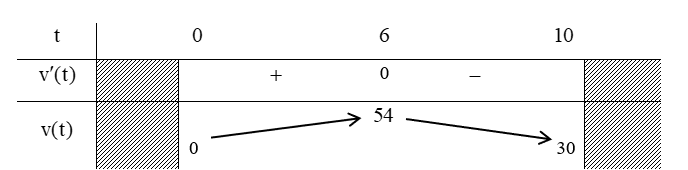
Dựa vào bảng biến thiên, ta thấy vận tốc lớn nhất của vật trong khoảng 10 giây đầu là \(54\) m/s.
I. Nhận biết
Cho hàm số y = f(x), nếu x thay đổi từ x1 đến x2 thì:
Giả sử chi phí C(x) (nghìn đồng) để sản xuất x bánh mì của một cửa hàng bánh được cho bởi hàm số C(x) = 2,5x3 – 500x + 100 000. Hàm chi phí biên của cửa hàng để sản xuất 120 bánh mì là:
Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần. Gọi p (triệu đồng) là giá của mỗi ti vi, x là số ti vi. Khi đó hàm cầu là:
Nếu C = C(t) là nồng độ của một chất tham gia phản ứng hóa học tại thời điểm t. Tốc độ phản ứng tức thời (độ thay đổi của nồng độ) của chất đó tại thời điểm t là:
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là y = t3 – 12t + 3, (t ≥ 0). Quãng đường hạt đi được trong khoảng thời gian 0 < t < 3 là
</>
Cho chuyển động thẳng xác định bởi phương trình s = t3 – 3t2 + 4t trong đó t tính bằng giây (s) và s được tính bằng mét (m). Gia tốc của chất điểm lúc t = 2 s bằng:
II. Thông hiểu
Một tên lửa bay vào không trung với quãng đường đi được \(s\left( t \right) = {e^{{t^2} + 3}} + 2t.{e^{3t + 1}}\) (km). Hỏi vận tốc của tên lửa sau 1 giây là bao nhiêu?
Một vật chuyển động trên một đường thẳng theo quy luật s = s(t), khi đó biểu thức biểu thị vận tốc tức thời của vật là:
Quy trình giải một bài toán tối ưu hóa được thực hiện theo các bước sau:
(1) Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
(2) Chọn một đại lượng thích hợp nào đó, kí hiệu là x và biểu diễn các đại lượng khác theo x. Khi đó đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số Q = Q(x).
(3) Tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số Q = Q(x) bằng các phương pháp đã biết và kết luận.
Thứ tự các bước đúng là:
Một vật rơi tự do với phương trình chuyển động \(s = \frac{1}{2}g{t^2}\) trong đó g = 9,8 m/s2 và t tính bằng giây (s). Vận tốc của vật tại thời điểm t = 5 s bằng:
Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288\,\,\,d{m^3}\]. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,000\] đồng/\({m^2}\). Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định được số lượng vi khuẩn tăng theo thời gian bởi qui luật \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con vi khuẩn), trong đó t là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào, số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu?
Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số \(P\left( t \right) = \frac{{25{t^2} + 125}}{{{t^2} + 1}}\), (0 ≤ t ≤ 10) trong đó thời gian t được tính bằng giây. Tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim là:
Một vật chuyển động theo quy luật \(s = {t^3} + \frac{3}{2}{t^2} + 1\), với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Vận tốc tức thời của vật là:
