Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau.

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm này ? (Làm tròn kết quả đến hàng phần trăm).
A. \(0,06.\)
B. \(0,08.\)
C. \(0,07.\)
D. \(0,09.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Cỡ mẫu \(n = 21 + 39 + 55 + 26 + 9 = 150.\)
Ta có: \(\frac{n}{4} = 37,5\) nên nhóm chứa tứ phân vị thức nhất là \(\left[ {0,95;1,0} \right)\).
Do đó, \({Q_1} = 0,95 + \frac{{37,5 - 21}}{{39}}\left( {1,0 - 0,95} \right) = \frac{{101}}{{104}}.\)
Ta có: \(\frac{{3n}}{4} = 112,5\) nên nhóm chứa tứ phân vị thứ ba là \(\left[ {1,0;1,05} \right)\).
Do đó, \({Q_3} = 1,0 + \frac{{112,5 - \left( {21 + 39} \right)}}{{55}}\left( {1,05 - 1,0} \right) = \frac{{461}}{{440}}.\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
\(\Delta Q = {Q_3} - {Q_1} = \frac{{461}}{{440}} - \frac{{101}}{{104}} \approx 0,08.\)
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).

Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

Khi đó:
a) Cỡ mẫu \(n = 100.\)
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là \({Q_1} = \frac{{683}}{{38}}.\)
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \(\Delta Q = \frac{{515}}{{114}}.\)
d) Biết rằng trong 100 lần đi trên, chỉ có đúng lần một lần ông Thắng đi hết hơn 29 phút. Thời gian của lần đi đó là giá trị ngoại lệ của mẫu số liệu ghép nhóm.
Số mệnh đề đúng là:
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.
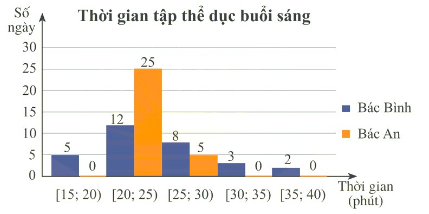
Xét các mệnh đề dưới đây:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là 25 (phút).
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là \(\Delta Q = 2.\)
c) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là \({Q_3} = \frac{{455}}{{16}}\).
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An lớn hơn bác Bình.
Số mệnh đề đúng là:
Bảng sau biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
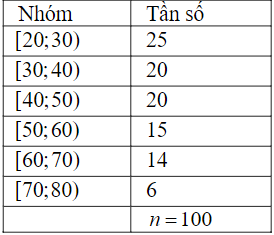
Khi đó:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: \(R = 60.\)
b) Tứ phân vị thứ nhất là: \({Q_1} = 35.\)
c) Tứ phân vị thứ ba là: \({Q_3} = \frac{{160}}{3}.\)
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là: \(\Delta Q = \frac{{65}}{3}.\)
Số mệnh đề đúng trong các mệnh đề trên là:
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Nhóm chứa tứ phân vị thứ nhất là:
III. Vận dụng
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
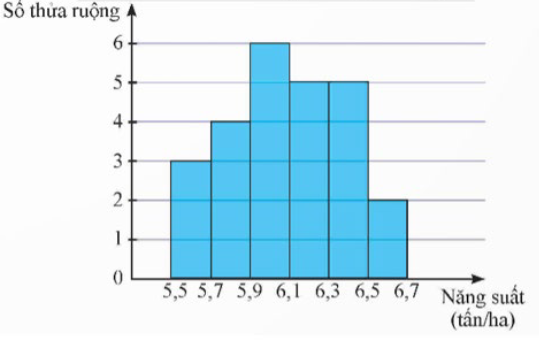
Khi đó:
a) Có 25 thửa ruộng đuộc khảo sát.
b) Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
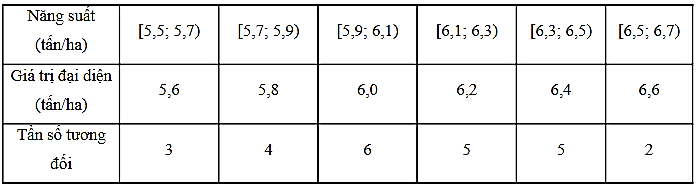
c) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 0,4675.
Số mệnh đề đúng trong các mệnh đề trên là:
I. Nhận biết
Gọi \({Q_1},{Q_2},{Q_3}\) là tứ phân vị thứ nhất, tứ phân vị thứ hai và thứ ba của mẫu số liệu ghép nhóm. Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
Nếu so sánh theo khoảng tứ phân vị thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
Điểm kiểm tra giữa học kì 1 của một nhóm học sinh được thống kê như bảng sau:

Khoảng tứ phân vị của mẫu số liệu trên:
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm này là
II. Thông hiểu
Nếu so sánh theo khoảng biến thiên thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây:
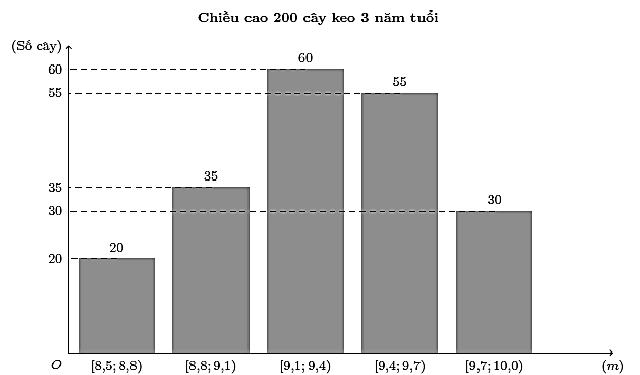
Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên là (kết quả làm tròn đến chữ số hàng thập phân thứ hai):
Bốn bạn Ánh, Ba, Châu, Dũng cùng là thành viên của một câu lạc bộ rubik. Trong một lần luyện tập rubik với nhau, mỗi bạn đã cùng giải rubik 30 lần liên tiếp và thống kê kết quả lại ở bảng sau:
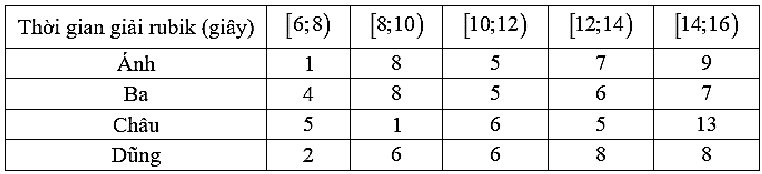
Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì bạn nào có tốc độ giải rubik đồng đều nhất?
Bảng sau thống kê khối lượng một quả cam được chọn ngẫu nhiên trong một thùng hàng.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: