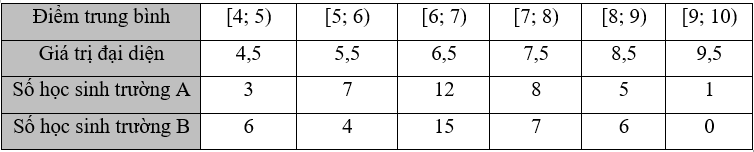
Khảo sát điểm trung bình năm học của hai nhóm học sinh lớp 12 ngẫu nhiên của hai trường A và B ta được mẫu số liệu ghép nhóm sau:
Khi đó:
a) Nếu so sánh theo khoảng biến thiên thì điểm trung bình năm của học sinh trường B đồng đều hơn.
b) Điểm trung bình của học sinh trường A cao hơn điểm trung bình của học sinh trường B.
c) Nếu so sánh theo khoảng tứ phân vị thì học sinh trường A học đều hơn.
d) Nếu so sánh theo độ lệch chuẩn thì học sinh trường A đồng đều hơn.
Số mệnh đề đúng trong các mệnh đề trên là:
A. \(1.\)
B. \(2.\)
C. \(3.\)
D. \(4.\)
Giải bởi Vietjack
Đáp án đúng là: B
a)
Xét về khoảng biến thiên:Khoảng biến thiên về điểm trung bình của học sinh trường A là:
\({R_A} = 10 - 4 = 6\) (điểm).
Khoảng biến thiên về điểm trung bình của học sinh trường B là:
\({R_B} = 9 - 4 = 5\) (điểm).
Do đó, nếu so sánh theo khoảng biến thiên thì điểm trung bình năm của học sinh trường B đồng đều hơn.
Vậy ý a đúng.
b) Số điểm trung bình của học sinh trường A là:
\(\overline {{x_A}} = \frac{{3.4,5 + 7.5,5 + 12.6,5 + 8.7,5 + 5.8,5 + 1.9,5}}{{3 + 7 + 12 + 8 + 5 + 1}} \approx 6,72.\)
Số điểm trung bình của học sinh trường B là:
\(\overline {{x_B}} = \frac{{6.4,5 + 4.5,5 + 15.6,5 + 7.7,5 + 6.8,5}}{{6 + 4 + 15 + 7 + 6}} \approx 6,58.\)
Vậy điểm trung bình của học sinh trường A cao hơn điểm trung bình của học sinh trường B.
Do đó ý b đúng.
c) Xét về khoảng tứ phân vị
Với học sinh trường A:
Cỡ mẫu: \(n = 3 + 7 + 12 + 8 + 5 + 1 = 36\).
Ta có: \(\frac{n}{4} = \frac{{36}}{4} = 9\) nên nhóm chứa tứ phân vị thứ nhất là \(\left[ {5;6} \right)\).
Do đó, \({Q_1} = 5 + \frac{{9 - 3}}{7}\left( {6 - 5} \right) = \frac{{41}}{7}.\)
Ta có: \(\frac{{3n}}{4} = \frac{{3.36}}{4} = 27\) nên nhóm chứa tứ phân vị thứ ba là \(\left[ {7;8} \right)\).
Do đó, \({Q_3} = 7 + \frac{{27 - \left( {3 + 7 + 12} \right)}}{8}\left( {8 - 7} \right) = \frac{{61}}{8}\).
Khoảng tứ phân vị của mẫu số liệu trường A là:
\(\Delta Q = {Q_3} - {Q_1} = \frac{{61}}{8} - \frac{{41}}{7} = \frac{{99}}{{56}} \approx 1,77.\)
Với học sinh trường B:
Cỡ mẫu: \(n = 6 + 4 + 15 + 7 + 6 = 38\).
Ta có: \(\frac{n}{4} = \frac{{38}}{4} = 9,5\) nên nhóm chứa tứ phân vị thứ nhất là \(\left[ {5;6} \right)\).
Do đó, \({Q_1} = 5 + \frac{{9,5 - 6}}{4}\left( {6 - 5} \right) = 5,875.\)
Ta có: \(\frac{{3n}}{4} = \frac{{3.38}}{4} = 28,5\) nên nhóm chứa tứ phân vị thứ ba là \(\left[ {7;8} \right)\).
Do đó, \({Q_3} = 7 + \frac{{28,5 - \left( {6 + 4 + 15} \right)}}{7}\left( {8 - 7} \right) = 7,5.\)
Khoảng tứ phân vị của mẫu số liệu trường B là:
\(\Delta Q = {Q_3} - {Q_1} = 7,5 - 5,875 = 1,625.\)
Vậy nếu so sánh theo khoảng tứ phân vị thì học sinh trường B học đều hơn.
Do đó ý c sai.
d) Độ lệch chuẩn của mẫu số liệu của trường A là:
\({s_A} = \sqrt {\frac{{3.4,{5^2} + 7.5,{5^2} + 12.6,{5^2} + 8.7,{5^2} + 5.8,{5^2} + 1.9,{5^2}}}{{36}} - 6,{{72}^2}} \approx 1,239.\)
Độ lệch chuẩn của mẫu số liệu trường B là:
\({s_B} = \sqrt {\frac{{6.4,{5^2} + 4.5,{5^2} + 15.6,{5^2} + 7.7,{5^2} + 6.8,{5^2}}}{{38}} - 6,{{58}^2}} \approx 1,238.\)
Nếu so sánh theo độ lệch chuẩn thì học sinh trường B đồng đều hơn.
Vậy ý d sai.
Cân nặng của một quả mít trong một khu vườn được thông kê ở bảng sau:
Số trung bình của mẫu số liệu ghép nhóm trên là:
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết pin của một số máy vi tính cùng loại được mô tả ở biểu đồ trên.
Phương sai của thời gian sử dụng pin gần nhất với giá trị nào dưới đây?
Một phòng khám thống kê số bệnh nhân đến khám bệnh mỗi ngày trong một tháng ở bảng sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần nhất với kết quả nào dưới đây ?
II. Thông hiểu
Nhiệt độ trong 55 ngày của một địa phương được cho trong bảng số liệu sau:
Phương sai của mẫu số liệu được làm tròn đến chữ số thập phân thứ nhất nằm trong khoảng
Một giáo viên ghi lại điểm kiểm tra học kì I môn Toán của hai lớp 12A và 12B vào mẫu số liệu ghép nhóm sau:
Khi đó:
a) Sĩ số học sinh hai lớp 12A và 12B bằng nhau.
b) Điểm kiểm tra trung bình của hai lớp chênh lệch nhau không quá 0,5 điểm.
c) Nếu xét theo khoảng biến thiên thì điểm kiểm tra của lớp 12B đồng đều hơn.
d) Nếu xét theo độ lệch chuẩn thì điểm kiểm tra của lớp 12A lại đồng đều hơn.
Số mệnh đề đúng trong các mệnh đề trên là:
Một mẫu số liệu ghép nhóm có phương sai bằng 25 thì có độ lệch chuẩn bằng:
Bảng sau thống kê số lượt chở khách mỗi ngày của một tài xế taxi trong 30 ngày:
Độ lệch chuẩn \(S\) của mẫu số liệu trên thỏa mãn:
Khối lượng 66 quả bưởi da xanh ở lô hàng A được ghi lại ở bảng sau:
Khối lượng trung bình của mỗi quả bưởi gần nhất với kết quả nào dưới đây:
Thành tích môn nhảy cao của các vận động viên tại một giải điền kinh danh cho học sinh học phổ thông như sau:
Độ lệch chuẩn của mẫu số liệu được làm tròn đến chữ số thập phân thứ hai là
I. Nhận biết
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng 4 thì có phương sai bằng
Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên có giá trị gần nhất với giá trị nào sau đây:
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần như sau:
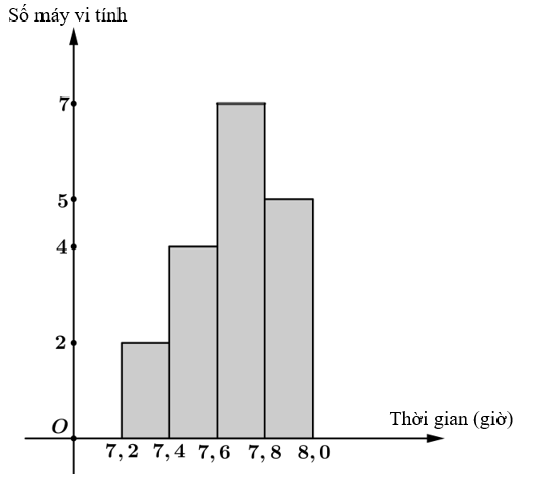
Phương sai của mẫu số liệu ghép nhóm trên là (làm tròn đến hàng đơn vị):
Một phòng thu âm thống kê độ to của 100 bài nhạc (đơn vị: dB) khi mở max âm lượng của một cái loa như bảng sau:
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây ?
Số lượng khách hàng nữ mua hàng thời trang trong một ngày của một cửa hàng được thống kê trong bảng tần số ghép nhóm sau:
Khi đó:
a) Cỡ mẫu là \(n = 20.\)
b) Giá trị đại diện của nhóm \(\left[ {30;40} \right)\) là \(35.\)
c) Số trung bình của mẫu số liệu ghép nhóm trên là 42,08 (đã làm tròn đến hàng phần trăm).
d) Phương sai của mẫu số liệu ghép nhóm là 19,99 (làm tròn đến hàng phần trăm).
Số mệnh đề đúng trong các mệnh đề trên là:
Biết trong một trò chơi thể thao điện tử, có một chỉ số quan trọng là chỉ số DPS, biểu thị lượng sát thương gây ra mỗi giây. Lượng DPS trung bình của mỗi trận của hai xạ thủ A và B được thống kê qua 32 trận đấu tập luyện như sau:
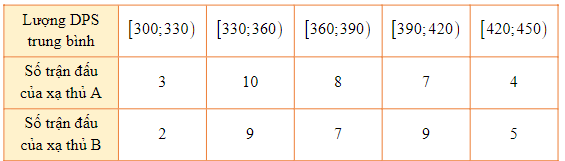
Khi đó:
a) Nếu xét về khoảng biến thiên thì lượng DPS trung bình của hai xạ thủ đồng đều nhau.
b) Biết giá trị trung bình sau 32 trận đấu tập của lượng DPS trung bình mỗi trận của mỗi xạ thủ trên 380 là đạt yêu cầu tập luyện. Vậy cả 2 xạ thủ trên đều đạt yêu cầu tập luyện.
c) Số trận đấu có lượng DPS trung bình mỗi trận dưới 360 của hai xạ thủ bằng nhau.
d) Nếu xét theo độ lệch chuẩn thì lượng DPS trung bình của xạ thủ A đồng đều hơn xạ thủ B.
