X là ĐLNN có hàm mật độ xác suất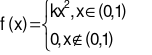

Với 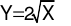. Thì xác suất P(Y>1) là:

Một xạ thủ có 4 viên đạn, anh ta bắn lần lượt từng viên cho đến khi trúng mục tiêu hoặc hết cả 4 viên thì thôi biết xác suất trúng đích là 0.7. Gọi X là số viên đạn đã bắn. Mốt Mod[X] bằng:

Xác suất để một người bị phản ứng từ việc tiêm huyết thanh là 0,001. Xác suất để trong 2000 người tiêm huyết thanh, có đúng 3 người bị phản ứng:

Theo dõi thời gian hoàn thành sản phẩm của 50 công nhân ta có bảng số liệu sau:

Thời gian hoàn thành sản phẩm trung bình của công nhân là:

Lấy 2 sản phẩm từ một hộp chứa 10 sản phẩm trong đó có 2 phế phẩm. X là biến ngẫu nhiên chỉ số phế phẩm trong 2 sản phẩm trên. Bảng phân phối xác suất của X là:

Hàm mật độ của biến ngẫu nhiên X cho bởi:

Có 3 hộp, mỗi hộp đựng 5 viên bi, trong đó hộp thứ nhất có 1 bi trắng; hộp thứ hai có 2 bi trắng; hộp thứ ba có 3 bi trắng. Chọn ngẫu nhiên một hộp rồi từ hộp đó lấy ngẫu nhiên ra 3 bi (lấy không hoàn lại). Tìm xác suất để lấy được 3 bi trắng.

Một người có 3 chỗ ưa thích như nhau để câu cá. Xác suất câu được một con cá ở chỗ thứ nhất, thứ hai, thứ ba tương ứng là 0,6; 0,7; 0,8. Biết rằng ở mỗi chỗ, người đó đã thả câu 3 lần và có một lần câu được cá. Tính xác suất để đó là chỗ thứ nhất.

Ba xạ thủ cùng bắn 1 con thú (mỗi người bắn 1 viên đạn). Xác suất bắn trúng của từng người tương ứng là 0,6; 0,7; 0,8. Biết rằng nếu trúng 1 phát đạn thì xác suất để con thú bị tiêu diệt là 0,5; trúng 2 phát đạn thì xác suất để con thú bị tiêu diệt là 0,8; còn nếu trúng 3 phát đạn thì chắc chắn con thú bị tiêu diệt.Tính xác suất để con thú bị tiêu diệt.

Một hộp đựng 5 chai thuốc trong đó có 1 chai thuốc giả. Người ta lần lượt kiểm tra từng chai cho đến khi phát hiện được chai thuốc giả thì thôi (giả thiết các chai thuốc phải qua kiểm tra mới xác định được là thuốc giả hay tốt). Thì luật phân phối xác suất của số chai thuốc được kiểm tra theo công thức:

Một cửa hàng bán một loại sản phẩm trong đó 40% do phân xưởng 1 sản xuất, còn lại do phân xưởng 2 sản xuất. Tỷ lệ sản phẩm A do phân xưởng 1 và 2 sản xuất tương ứng là 0,8; 0,9. Mua ngẫu nhiên 1 sản phẩm từ cửa hàng và thấy đó không phải sản phẩm loại

Một bình chứa 10 bi, và có 5 bi đỏ, 3 bi vàng. Lấy NN lần I ra 1 bi để trên bàn, sau đó lấy lần II ra 2 bi nữa để trên bàn. Tính XS để lần II lấy ra chỉ được 2 bi đỏ.

Tuổi thọ X của một loại sản phẩm (giờ) là một biến ngẫu nhiên liên tục có hàm mật độ xác suất là

Tuổi thọ trung bình của sản phẩm là:

Một người có 4 cái quần khác nhau, 6 cái áo khác nhau, 3 chiếc cà vạt khác nhau. Để chọn một cái quần hoặc một cái áo hoặc một cái cà vạt thì số cách chọn khác nhau là:

Đại lượng ngẫu nhiên X có phân bố xác suất như sau:

Xét biến ngẫu nhiên Y = min{X, 4}. Khi đó P(Y = 4) =?

Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn một học sinh ở khối 11 đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?