Xét giả thuyết H0: “sinh viên A có điểm tổng kết môn Xác suất thống kê dưới 4”. Diễn đạt sai lầm loại 1 khi kiểm định
A. A đạt môn Xác suất thống kê nhưng không được công nhận
B. A không đạt nhưng vẫn cho đạt môn Xác suất thống kê
C. A đạt môn Xác suất thống kê
D. A không đạt môn xác suất thống kê
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án C
Nếu mẫu lấy ra từ tổng thể có phân phối chuẩn phương sai chưa biết thì: 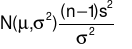
Một chiếc hộp đựng 5 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên lần lượt ra 2 viên. Xác suất để lần 2 lấy được viên phấn trắng là bao nhiêu. Biết lần 1 đã lấy được phấn trắng?
Kiểm tra 2000 hộ gia đình. Để điều tra nhu cầu tiêu dùng một loại hàng hóa tại vùng đó, người ta nghiên cứu ngẫu nhiên 100 gia đình và thấy có 60 gia đình có nhu cầu về loại hàng hóa nói trên.Với độ tin cậy 95%. Ước lượng bằng khoảng tin cậy đối xứng số gia đình trong vùng có nhu cầu về loại hàng hóa nói trên?
Đo chiều cao X (cm) của 9 sinh viên, ta được kết quả: 152; 167; 159; 171; 162; 158; 156; 165 và 166.Tính S (độ lệch mẫu hiệu chỉnh)
Một máy bay đang bay sẽ bị rơi khi cả 2 dộng cơ bị hỏng hoặc phi công điều khiển bị mất hiệu lực lái. Biết xác suất để động cơ thứ nhất hỏng là 0,2; của dộng cơ thứ 2 là 0,3. Xác suất để máy bay rơi là:
Ước lượng số cá trong hồ, đánh bắt 200 con cá đánh dấu và thả xuống hồ. Sau đó đánh bắt 1600 con thấy có 80 con được đánh dấu. Với độ tin cậy bằng 0,9, hãy ước lượng số cá hiện có trong hồ?
Giả sử 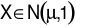 . Lấy mẫu với n = 16 ta tính được
. Lấy mẫu với n = 16 ta tính được 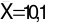 . Hãy kiểm định giả thuyết
. Hãy kiểm định giả thuyết 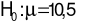 với mức ý nghĩa 5%
với mức ý nghĩa 5%
Trong một chiếc hộp có đựng 7 chính phẩm và 3 phế phẩm. Lấy ngẫu nhiên lần lượt ra 2 sản phẩm theo cách không hoàn lại. Xác suất để cả 2 sản phẩm đều là chính phẩm là:
Để biểu diễn quy luật phân phối của biến ngẫu nhiên người ta dùng:
Kích thước một loại sản phẩm là 1 BNN phân phối chuẩn. Kiểm tra 15 sản phẩm ta có s=14,6. Sản phẩm được coi là đạt tiêu chuẩn nếu. Với ta cho rằng chất lượng sản phẩm thế nào? Xσ=12α=5%
Kiểm tra 400 sản phẩm thì thấy 160 sản phẩm loại I. Ước lượng tỉ lệ sản phẩm loại I tối đa với độ tin cậy 95%?
Lớp A có 41 sinh viên và lớp B có 31 sinh viên. Kết quả thi môn xác suất của 2 lớp là gần giống hau, lớp A có độ lệch chuẩn là 12, lớp B có độ lệch chuẩn là 9. Có ý kiến cho rằng lớp B đồng đều hơn lớp A về điểm thi môn này. Ta dùng bài toán kiểm định nào để kết luận với mức ý nghĩa 5%
Một mẫu gồm 200 sinh viên được chọn ngẫu nhiên và tính được tuổi trung bình của họ là 22,4 (năm) và độ lệch chuẩn của mẫu đó bằng 3 (năm). Để ước lượng khoảng tin cậy của tuổi trung bình của sinh viên thì phân phối nào sau đây được sử dụng?