 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời: 1
Ta có 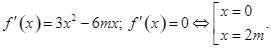
Bảng biến thiên
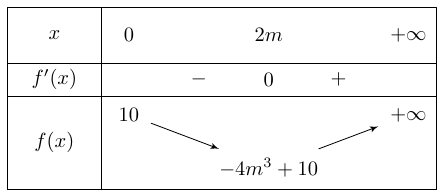
Dựa vào bảng biến thiên ta thấy ![]() khi
khi ![]() .
.
Theo giả thiết ta có ![]() .
.
Vậy ![]() thỏa yêu cầu bài toán.
thỏa yêu cầu bài toán.
Thời gian tập nhảy mỗi ngày trong thời gian gần đây của Cô Minh Hiền được thống kê lại ở bảng sau:
![]()
Khoảng biến thiên của mẫu số liệu ghép nhóm là
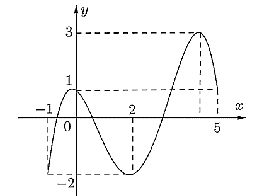
Cho hàm số ![]() liên tục trên
liên tục trên ![]() và có đồ thị trên đoạn
và có đồ thị trên đoạn ![]() như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() có đồ thị như hình vẽ dưới đây:
có đồ thị như hình vẽ dưới đây:
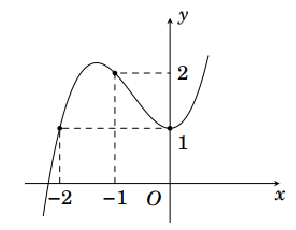
a) Hàm số đồng biến trên khoảng ![]() .
.
b) Hàm số đạt cực tiểu tại ![]() .
.
c) Đồ thị hàm số cắt trục Oy tại điểm có tọa độ ![]() .
.
d) ![]() .
.
Cho hàm số ![]() có đồ thị
có đồ thị ![]() .
.
a) Hàm số nghịch biến trên khoảng ![]() ∪
∪ ![]() .
.
b) Giá trị nhỏ nhất của hàm số trên đoạn ![]() bằng
bằng ![]() .
.
c) Đồ thị hàm số ![]() có tiệm cận xiên là đường thẳng
có tiệm cận xiên là đường thẳng ![]() .
.
d) Góc giữa hai đường tiệm cận của đồ thị hàm số bằng ![]() .
.
Trong không gian ![]() , cho hai vectơ
, cho hai vectơ ![]() và
và ![]() và điểm
và điểm ![]() .
.
a) Ta có ![]() .
.
b) Tọa độ vectơ ![]() .
.
c) Điểm đối xứng của ![]() qua Oy là
qua Oy là ![]() .
.
d) Góc giữa vectơ ![]() và
và ![]() nhỏ hơn
nhỏ hơn ![]() .
.
Thống kê lại thu nhập trong một tháng của nhân viên hai công ty A và B (đơn vị: triệu đồng) được thể hiện trong biểu đồ dưới đây
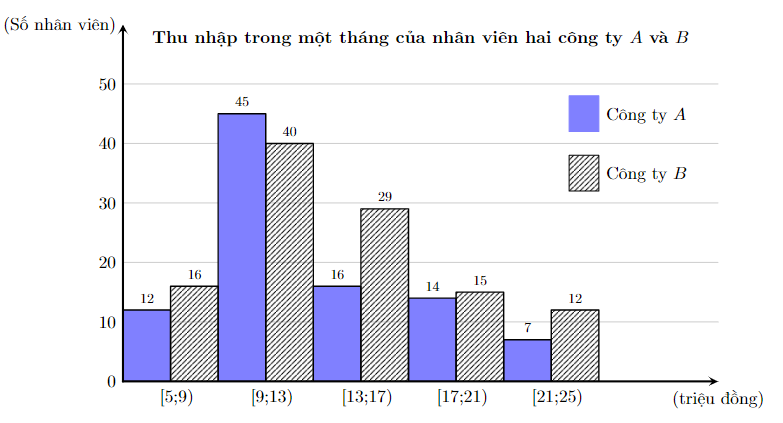
a) Có 14 nhân viên của công ty A thu nhập từ 17 triệu đồng đến 21 triệu đồng trong một tháng.
b) Thu nhập trung bình mỗi tháng của nhân viên công ty A cao hơn nhân viên công ty B.
c) Nếu so sánh về phương sai thì thu nhập mỗi tháng của nhân viên công ty A ít phân tán hơn nhân viên công ty B.
d) Nếu so sánh về khoảng tứ phân vị thì thu nhập trung bình mỗi tháng của công ty B đồng đều hơn công ty A.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() xác định trên
xác định trên ![]() và có bảng biến thiên như hình vẽ sau
và có bảng biến thiên như hình vẽ sau
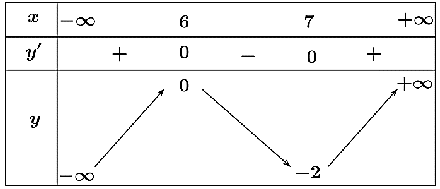
Điểm cực đại của hàm số ![]() là
là
Cho hàm số ![]() có bảng biến thiên như sau
có bảng biến thiên như sau
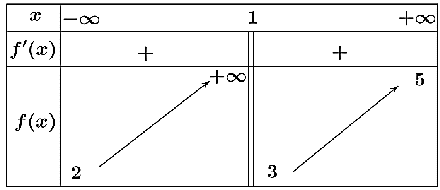
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là