Tập hợp các điểm biểu diễn số phức z sao cho là một số thuần ảo.
Là một đường tròn tâm I(a;b). Tính tổng a + b
A. 2
B. 1
C. -2
D. 3
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
Giả sử ![]() có điểm M(x;y) biểu diễn z trên mặt phẳng (Oxy).
có điểm M(x;y) biểu diễn z trên mặt phẳng (Oxy).
Khi đó
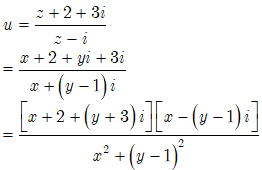
Từ số bằng: ![]() ; u là số thuần ảo khi và chỉ khi:
; u là số thuần ảo khi và chỉ khi:
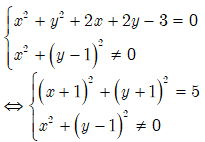
Kết luận: Vậy tập hợp các điểm biểu diễn của z là một đường tròn tâm I(-1;-1), bán kính R=, loại đi điểm (0;1).
Cho số phức z thỏa mãn (1-3i)z+1+i=-z. Môđun của số phức w=13z+2i có giá trị bằng:
Trong mặt phẳng Oxy, M,N,P là tọa độ điểm biểu diễn của số phức
Tọa độ trực tâm H của tam giác MNP là:
Trong mặt phẳng tọa độ Oxy, cho ba điểm M,N,P là điểm biểu diễn của 3 số phức: .Với giá trị nào của x thì tam giác MNP vuông tại P?
Cho các số phức được biểu diễn trong mặt phẳng tọa độ Oxy là M,N,P, các điểm này lần lượt là trung điểm của ba cạnh tam giác EFH. Tọa độ trọng tâm G của tam giác EFH là:
Trên mặt phẳng tọa độ Oxy . Cho tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện . Phát biểu nào sau đây là sai:
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn và biểu thức . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
Gọi T là tập hợp các số phức z thỏa mãn và . Gọi lần lượt là các số phức có môdun nhỏ nhất và lớn nhất. Tìm số phức