Diện tích hình phẳng giới hạn bởi đồ thị hàm số y , trục hoành, đường thẳng x = -1 và đường thẳng x = -2 là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Diện tích giới hạn được tính bởi
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số và y = 6 - x và trục tung là
Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số , trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox
Vận tốc của một vật chuyển động là (m/s). Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:
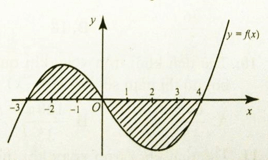
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và đồ thị hàm số
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành, đường thẳng x = -1 và đường thẳng x = 1.
Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và
Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?
Thể tích khối xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = x(x-4) và trục hoành là:
Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.
Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:
Thể tích khối tròn khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số là:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.