Cho hình chóp S.ABC có đáy là tam giác vuông tại A, các cạnh AB = 1, AC = 2. Các tam giác SAB và SAC lần lượt vuông tại B và C. Góc giữa (SBC) và mặt phẳng đáy bằng 60°. Tính thể tích của khối chóp đã cho.
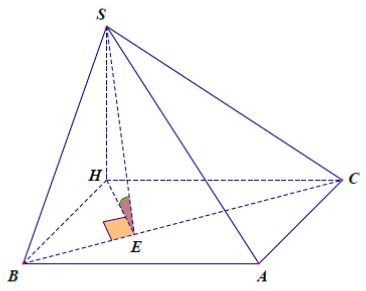
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack

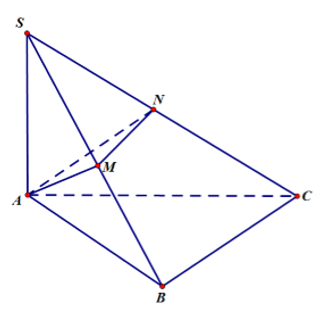
Cho hình chóp S.ABC có (SAB),(SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên SB tạo với đáy một góc 60° đáy ABC là tam giác vuông cân tại B với BA = BC = a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện A.BMNC
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a; . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:

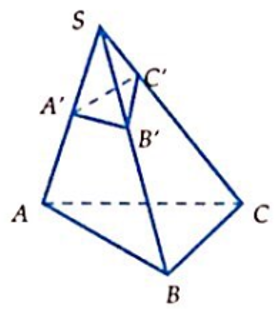
Cho khối chóp S.ABC có SA = 9, SB = 4, SC = 8 và đôi một vuông góc. Các điểm A', B', C' thỏa mãn . Thể tích khối chóp S.A'B'C' là:
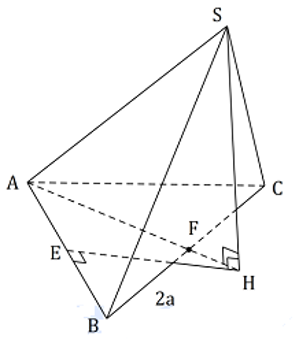
Cho hình chóp S.ABC có SA = SB = SC = a và đáy là tam giác ABC cân tại A. Biết và BC = 2a. Thể tích khối chóp S.ABC là
Mỗi hình dưới đây gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó).
Số đa diện lồi trong các hình vẽ trên là:
Cho khối chóp tứ giác đều S.ABCD có cạnh bằng a, cạnh bên SC tạo với mặt đáy một góc 45°. Tính thể tích của khối chóp S. ABCD
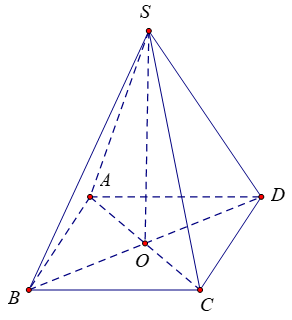
Tính thể tích của hình hộp ABCD.A'B'C'D' biết rằng AA'B'D' là tứ diện đều cạnh bằng a.
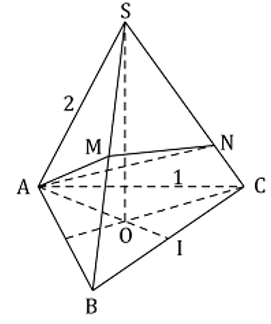
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, các cạnh bên bằng 2a. Gọi M là trung điểm SB, N là điểm trên cạnh SC sao cho SN = 3NC. Thể tích khối chóp A.BCNM có giá trị nào sau đây?
Cho hình chóp tam giác đều cạnh bằng 3. Tính thể tích hình chóp đó biết chiều cao h = 7
Mỗi cạnh của một khối đa diện là cạnh chung của bao nhiêu mặt của khối đa diện:
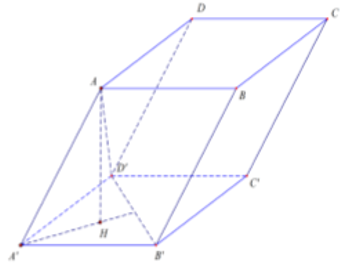
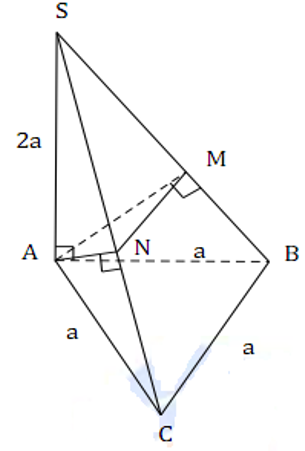
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a, SC tạo với mặt phẳng đáy (ABCD) một góc 60°. Thể tích khối chóp S.ABCD theo a là
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và thể tích V = 12 c. Mặt bên SAB là tam giác đều cạnh bằng 4cm. Tính khoảng cách từ C đến mặt phẳng (SAB).
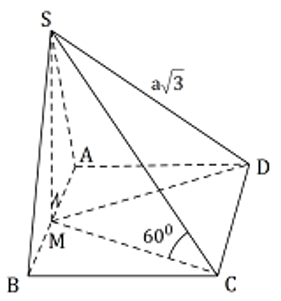
Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng: