Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:

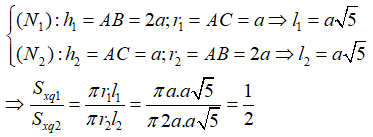
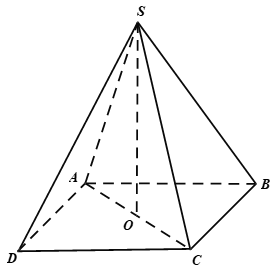
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60°. Tính diện tích xung quanh S_xq của hình nón đỉnh S có đáy là hình tròn ngoại tiếp tam giác ABC.

Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc $\widehat{\mathrm{SAB}}$ = 60°. Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:

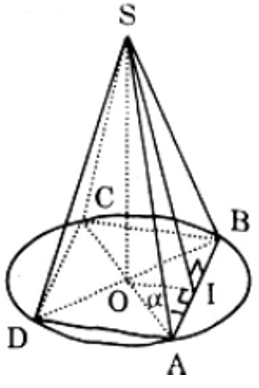
Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = $\sqrt{3}$ và góc $\widehat{\mathrm{SAB}}$ = α = 60°. Tính diện tích xung quanh của hình nón đỉnh S đáy là đường tròn ngoại tiếp tứ giác ABCD

Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:

Cho hình nón S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S và cắt đường tròn đáy tại A và B sao cho AB = 2$\sqrt{3}$a Tính khoảng cách d từ tâm của đường tròn đáy đến (P)

Cho khối nón tròn xoay có góc ở đỉnh là 60^o và đường sinh l = 6cm. Thể tích của khối nón là:

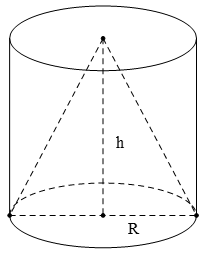
Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích ${\mathrm{V}}_1$; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích ${\mathrm{V}}_2$.

Khẳng định nào sau đây là khẳng định đúng ?

Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là:

Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.

Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng:

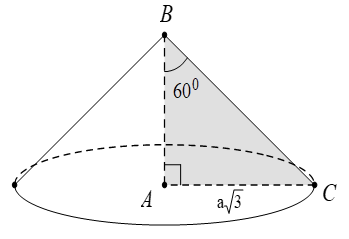
Hình nón có góc ở đỉnh là 9$0^{\mathrm{o}}$ và có diện tích xung quanh là π$\sqrt{2}$. Độ dài đường cao của hình nón là:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SC = a$\sqrt{6}$. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là: