Cho tam giác ABC vuông tại A (AB < AC), tia phân giác BM (M ∈ AC). Vẽ MK vuông góc với BC tại K. gọi N là giao điểm của MK và AB. Chứng minh:
a. BM là đường trung trực của AK
 Giải bởi Vietjack
Giải bởi Vietjack
a. Hình vẽ (0.5 điểm)
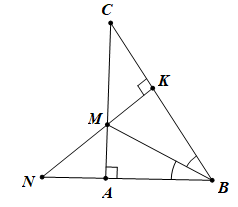
Xét ΔABM và ΔKBM có:
∠(ABM) = ∠(KBM)
BM là cạnh chung
⇒ ΔABM = ΔKBM(cạnh huyên – góc nhọn) (1 điểm)
⇒ AM = MK và BA = BK (hai cạnh tương ứng) ⇒ M, B nằm trên đường trung trực của AK (0.5 điểm)
Suy ra BM là đường trung trực của AK
Cho tam giác ABC, M là trung điểm của AC, G là trọng tâm của tam giác ABC và GM = 5cm. Độ dài đoạn BG là:
Cho tam giác ABC vuông tại A (AB < AC), tia phân giác BM (M ∈ AC). Vẽ MK vuông góc với BC tại K. gọi N là giao điểm của MK và AB. Chứng minh:
d. BM vuông góc với NC
B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có
a. So sánh AB và AC
A. Phần trắc nghiệm (3 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Trọng tâm của tam giác là:
Cho tam giác ABC vuông tại A (AB < AC), tia phân giác BM (M ∈ AC). Vẽ MK vuông góc với BC tại K. gọi N là giao điểm của MK và AB. Chứng minh:
b. MN = MC
Cho tam giác ABC vuông tại A (AB < AC), tia phân giác BM (M ∈ AC). Vẽ MK vuông góc với BC tại K. gọi N là giao điểm của MK và AB. Chứng minh:
c. AM < MC
Cho tam giác ABC vuông tại A có
b. Vẽ đường cao AH. Chứng minh HC > HB