Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
a. ΔABE = ΔBDE
 Giải bởi Vietjack
Giải bởi Vietjack
a. Hình vẽ (0.5 điểm)
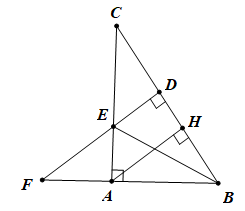
Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn) (1 điểm)
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
b. BE là đường trung trực của AD
Cho tam giác ABC, M là trung điểm của BC, G là trọng tâm của tam giác ABC và AM=12cm. Độ dài đoạn AG là:
B. Phần tự luận (7 điểm)
Cho tam giác DEF có DE < DF. Đường cao DH
a. So sánh HE và HF
Cho các bất đẳng thức sau, bất đẳng thức nào là bất đẳng thức tam giác?
Cho tam giác DEF có DE < DF. Đường cao DH
b. Lấy M ∈ DH. So sánh ME và MF
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC tại E, cắt BA tại F. Chứng minh
c. Tia BE là tia phân giác của (ABC)
Cho tam giác ABC không phải là tam giác cân. Khi đó trực tâm của tam giác ABC là giao điểm của:
A. Phần trắc nghiệm (3 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC có So sánh nào sau đây là đúng?