Tìm số nguyên m nhỏ nhất sao cho hàm số luôn nghịch biến trên các khoảng xác định của nó?
A. m = -1
B. m = -2
C. m = 0
D. Không có m
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D.
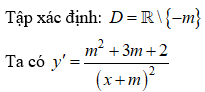
Để hàm số đã cho nghịch biến trên khoảng xác định:
⇔ y' < 0, ∀ x ∈ D ⇔ m2 + 3m + 2 < 0 ⇔ -2 < m < -1
Vậy không có số nguyên m nào thuộc khoảng (-2;-1).
Biết đồ thị hàm số có hai điểm cực trị A, B . Khi đó phương trình đường thẳng AB là:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên các khoảng mà nó xác định ?
Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R?
Tìm tất cả các giá trị của tham số m để hàm số đạt cực đại tại x = 1.