Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 = 0 và (Q): 8x - 6y - 1 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có:
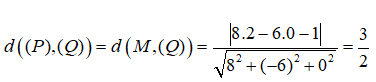
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz
Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 3z + 1 = 0 và mặt cầu (S): - 2x - 4y + 6z + 5 = 0. Khẳng định nào dưới đây là đúng?
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z - 1 = 0 và (Q): 3x + y + 2z - 3 = 0 là hai mặt phẳng có phương trình là:
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x - y + 2z = 0; 2x - 2y + ( + 3m)z + - m = 0, trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song?
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0; x - y + 2z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?
Trong không gian Oxyz, cho hai vectơ = (-1; 3; 4), = (2; -1; 5). Tích có hướng của hai vectơ và là:
Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:
Trong không gian Oxyz, cho mặt cầu (S): = 4 và mặt phẳng (P): 4x - 3y + m = 0. Với những giá trị nào của m thì mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung?
Trong không gian Oxyz, cho hai mặt phẳng: (P): x - 2y - 2z + 1 = 0, (Q): 2x - 4y - 4z + m = 0. Tìm các giá trị của m biết rằng khoảng cách giữa hai mặt phẳng (P) và (Q) bằng 1
Trong không gian Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P) có phương trình x - 2y + 2z + 1 = 0. Khoảng cách từ A đến mặt phẳng (P) là:
Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m - 6 = 0 và -2x + (5m + 1)y + (m + 3)z - 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:
Trong không gian Oxyz, biết rằng trục Ox song song với mặt phẳng (P): y + z - 1 = 0. Khoảng cách giữa Ox và mặt phẳng (P) là:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)