Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
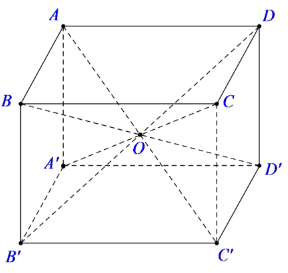
Dễ thấy tâm O của mặt cầu chính là tâm của hình lập phương.
Ta tính OA – bán kính mặt cầu.
Trong tam giác vuông ABC có: AC2 = AB2 + BC2 = 200.
Trong tam giác vuông AA'C có:
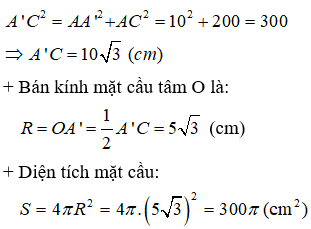
Trong không gian, cho tam giác ABC cân tại A, . Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.
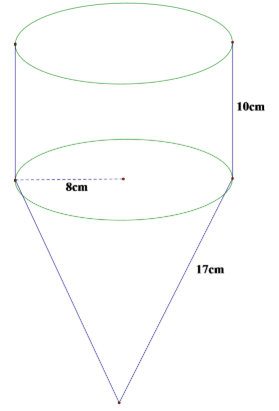
Một cái phễu rỗng phần trên có kích thước như hình vẽ. Diện tích xung quanh của phễu là:
I. Trắc nghiệm ( 6 điểm)
Một hình hộp chữ nhật có ba kích thước là a, b,c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Tính diện tích của hình cầu (S) theo a, b, c.
Trong không gian, cho tam giác ABC vuông tại A, AB = a và . Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB.
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD ?
Một hình trụ có hai đáy là hai hình tròn (O;r) và (O';r). Khoảng cách giữa hai đáy là . Một hình nón có đỉnh là O’ và có đáy là hình tròn (O;r). Mặt xung quanh của hình nón chia khối trụ thành 2 phần. Gọi là thể tích phần bên ngoài khối nón, là phần thể tích bên trong khối nón. Khi đó bằng:
Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông.
II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình tứ diện ABCD đều cạnh a.
Một hình nón có đường cao h = 20cm, bán kính đáy r = 25cm. Tính diện tích xung quanh của hình nón đó: