 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
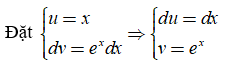
Theo công thức tính nguyên hàm từng phần, ta có:
![]()
F(x) là một nguyên hàm của hàm số . Hàm số nào sau đây không phải là F(x):
Một nguyên hàm của là kết quả nào sau đây, biết nguyên hàm này triệt tiêu khi x = 1?