Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.
a) Chứng minh ΔABH = ΔACH
b) Chứng minh AH ⊥ BC
c) Vẽ HD ⊥ AB (D ∈ AB) và HE ⊥ AC (E ∈ AC). Chứng minh: DE // BC
 Giải bởi Vietjack
Giải bởi Vietjack
a) Xét ΔABH và ΔACH có:
AH cạnh chung
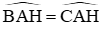
AB = AC (gt)
Suy ra: ΔABH = ΔACH (c – g – c)
b)
c) Gọi I là giao điểm của AH và DE
Xét hai tam giác vuông: ΔADH và ΔAEH có:
AH cạnh chung
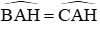
Suy ra: ΔADH = ΔAEH (ch – gn)
Xét ΔADI và ΔAEI có:
AI: cạnh chung
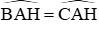
AD = AE (ΔADH = ΔAEH)
Suy ra: ΔADI = ΔAEI (c – g – c)
Nếu một đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc...... thì a//b. Cụm từ trong chỗ trống (...) là:
Trong các điểm sau, điểm nào thuộc đồ thị hàm số y = 2x.
Cho y tỉ lệ nghịch với x theo hệ số tỉ lệ là a, khi x = 3 thì y = 6. Vậy hệ số tỉ lệ a bằng:
Tính diện tích của một hình chữ nhật biết tỉ số giữa 2 kích thước của chúng là 0,8 và chu vi của hình chữ nhật đó là 36m.
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ –2 thì y và x liên hệ với nhau theo công thức: