Trong các hình sau đây hình nào vừa có tâm đối xứng, hình nào vừa có trục đối xứng: Hình chữ nhật, hình thang, hình bình hành, hình thoi, hình vuông, hình tròn, hình lục giác đều.
 Giải bởi Vietjack
Giải bởi Vietjack
- Hình chữ nhật có hai trục đối xứng là đường nối hai trung điểm của hai cạnh đối diện và tâm đối xứng là giao của hai đường chéo.
- Hình thang không có trục đối xứng, cũng ko có tâm đối xứng.
- Hình hình hành không có trục đối xứng và có tâm đối xứng là giao điểm của hai đường chéo.
- Hình thoi là hình có hai trục đối xứng là hai đường chéo và tâm đối xứng là giao điểm của hai đường chéo.
- Hình vuông có 4 trục đối xứng và tâm đối xứng là giao điểm của hai đường chéo.
- Hình tròn là hình có vô số trục đối xứng và có tâm đối xứng là tâm đường tròn.
- Hình lục giác đều có trục đối xứng và có tâm đối xứng là giao điểm của ba đường chéo chính.
Vậy các hình vừa có tâm đối xứng, hình nào vừa có trục đối xứng: Hình chữ nhật, hình thoi, hình vuông, hình tròn, hình lục giác đều.
Trong các hình: Hình bình hành, hình chữ nhật, hình vuông, hình lục giác đều, hình thoi thì có bao nhiêu hình không có tâm đối xứng?
Cho đoạn thẳng MN dài 18cm. Biết O là tâm đối xứng của MN. Tính ON
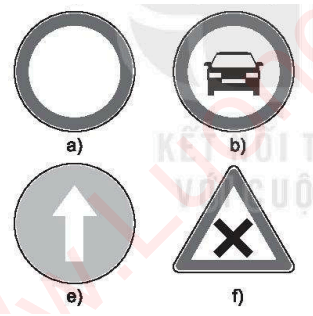
Trong các biển báo giao thông sau đây, biển nào có tâm đối xứng?
Các phát biểu sau đúng hay sai? Có bao nhiêu phát biểu sai?
a) Tam giác đều ABC là hình đối xứng tâm.
b) Hình thang cân là hình có tâm đối xứng và giao điểm của hai đường chéo là tâm đối xứng.
c) Hình thoi ABCD có tâm đối xứng là điểm O (O là giao điểm của hai đường chéo AC và BD).
Trong Hình 39, các hình từ hình a) đến e), hình nào có tâm đối xứng?

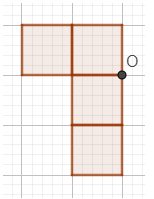
Em hãy vẽ thêm vào hình vẽ dưới đây để được hình có điểm O là tâm đối xứng: