A. x = 4cos(20t +\(\frac{\pi }{3}\)) (cm).
B. x = 4cos(20t +\(\frac{\pi }{3}\)) (cm).
C. x = 3cos(20t -\(\frac{\pi }{3}\)) (cm).
D. x = 3cos(20t -\(\frac{\pi }{3}\)) (cm).
Giải bởi Vietjack
+ Phương trình dao động của chất điểm có dạng: \[x = A\cos \left( {\omega t + \varphi } \right)\]
+ Chu kì dao động của chất điểm : \[T = \frac{t}{N} = \frac{{31,4}}{{100}} = \frac{\pi }{{10}}s\]
+ Tần số góc của dao động: \[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\](rad/s)
+ Biên độ dao động của chất điểm:
\[{A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} \Rightarrow A = \sqrt {0,{{02}^2} + \left( {\frac{{40\sqrt 3 {{.10}^{ - 2}}}}{{{{20}^2}}}} \right)} = 0,04m = 4cm\]
+ Tại t = 0, x = 2, v < 0 \[ \Rightarrow \varphi = \frac{\pi }{3}\]
Vậy phương trình dao động của vật là: \[x = 4\cos \left( {20t + \frac{\pi }{3}} \right)\](cm)
Chọn đáp án B
Một chất điểm thực hiện đồng thời hai dao động có phương trình li độ lần lượt là 
và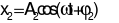 
. Biên độ dao động tổng hợp A được tính bằng biểu thức
Một con lắc đơn gồm vật nặng gắn vào dây treo dao động điều hoà với biên độ góc nhỏ. Chu kì của nó không phụ thuộc vào
, hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là
