Đề thi Giữa kì 1 Vật lí 12 có đáp án (Đề 4)
-
1809 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Một chất điểm thực hiện đồng thời hai dao động có phương trình li độ lần lượt là 
và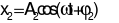 
. Biên độ dao động tổng hợp A được tính bằng biểu thức
Xem đáp án
Biên độ dao động tổng hợp A được tính bằng biểu thức:
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.cos\left( {{\varphi _2} - {\varphi _1}} \right)} \)
Chọn đáp án B
Câu 2:
Xem đáp án
Phương trình dao động điều hòa: x = 3cos(\[\pi t - \frac{\pi }{3})\]cm, có:
+ Biên độ dao động A = 3
+ Tần số góc: \[\omega = \pi \left( {{\rm{rad/s}}} \right)\]
+ Pha ban đầu: \[\varphi = - \frac{\pi }{3}\]
Chọn đáp án B
Câu 3:
Xem đáp án
Bước sóng là quãng đường sóng truyền được trong một chu kì hoặc khoảng cách giữa hai phần tử sóng gần nhất trên phương truyền sóng dao động cùng pha.
Chọn đáp án C
Câu 4:
Xem đáp án
Tần số góc trong dao động của con lắc lò xo: \[\omega = \sqrt {\frac{k}{m}} \left( {{\rm{rad/s}}} \right)\]
Chọn đáp án D
Câu 5:
Xem đáp án
Hiện tượng cộng hưởng chỉ xảy ra với dao động cưỡng bức.
Chọn đáp án B
Câu 6:
Xem đáp án
Hai nguồn kết hợp là hai nguồn dao động có cùng phương, cùng tần số và độ lệch pha không đổi.
Chọn đáp án C
Câu 7:
Xem đáp án
Trong dao động điều hoà, gia tốc biến đổi điều hoà ngược pha so với li độ: \[a = - {\omega ^2}x\]
Chọn đáp án D
Câu 8:
Xem đáp án
Chu kì dao động của con lắc lò xo: \[T = 2\pi \sqrt {\frac{m}{k}} \]
Chu kì dao động của con lắc không phụ thuộcvào biên độ dao động.
Chọn đáp án D
Câu 9:
tại nơi có gia tốc trọng trường g là Xem đáp án
Tần số dao động điều hoà của con lắc đơn: \[f = \frac{1}{{2\pi }}\sqrt {\frac{g}{\ell }} \]
Chọn đáp án B
Câu 10:
Xem đáp án
Biên độ dao động tổng hợp của haidao động cùng phương, cùng tần số thỏa mãn:
\[\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\]
\[ \Rightarrow \left| {5 - 8} \right| \le A \le 5 + 8 \Leftrightarrow 3 \le A \le 13\]
Chọn đáp án C
Câu 11:
Sóng dọc
Xem đáp án
Sóng dọc truyền được trong chất rắn, chất lỏng và chất khí.
Sóng ngang chỉ truyền được trong chất rắn và trên bề mặt chất lỏng.
Chọn đáp án B
Câu 12:
Một con lắc đơn gồm vật nặng gắn vào dây treo dao động điều hoà với biên độ góc nhỏ. Chu kì của nó không phụ thuộc vào
Xem đáp án
Ta có chu kỳ dao động của con lắc đơn là:
=> Chu kỳ chỉ phụ thuộc vào chiều dài con lắc ℓ và gia tốc trọng trường g mà gia tốc trọng trường phụ thuộc vào vĩ độ địa lý nên chu kỳ cũng phụ thuộc vào vĩ độ địa lý.
Chu kỳ không phụ thuộc vào khối lượng.
Chọn đáp án D
Câu 14:
, hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là Xem đáp án
Điều kiện có sóng dừng trên dây: \[\ell = k\frac{\lambda }{2}\]
Sóng dừng trên dây có bước sóng dài nhất ứng với kmin= 1 \[ \Rightarrow \lambda = 2\ell \]
Chọn đáp án D
Câu 15:
Xem đáp án
Hai điểm trên cùng một phương truyền sóng sẽ dao động cùng pha khi chúng cách nhau một khoảng d = k với k = 1, 2, 3, …
Chọn đáp án B
Câu 16:
Xem đáp án
+ Chu kì của con lắc đơn:\[T = 2\pi \sqrt {\frac{\ell }{g}} \]
Chu kì của nó không phụ thuộc vào khối lượng vật nặng.
+ Khi giảm chiều dài dây xuống 4 lần, tức là:\[\ell ' = \frac{\ell }{4}\]
+ Chu kì lúc sau của con lắc đơn là: \[T' = 2\pi \sqrt {\frac{{\ell '}}{g}} = 2\pi \sqrt {\frac{\ell }{{4g}}} = \frac{T}{2}\]
Chọn đáp án A
Câu 17:
Xem đáp án
Vì \[x \bot v \Rightarrow {\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\]
Biên độ A: \[{A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2}\]và vận tốc v: \[{v^2} = {\omega ^2}\left( {{A^2} - {x^2}} \right)\]
Chọn đáp án A
Câu 18:
Xem đáp án
+ Mối quan hệ giữa li độ và gia tốc trong dao động điều hòa: \[a = - {\omega ^2}x\]
+ Vì \[x \in \left[ { - A;A} \right] \Rightarrow a \in \left[ { - A{\omega ^2};A{\omega ^2}} \right]\]
Vậy đồ thị biểu diễn sự biến thiên của gia tốc theo li độ trong dao động điều hòa có dạng là đoạn thẳng.
Chọn đáp án B
Câu 19:
Xem đáp án
Dao động cơ học tắt dần có cơ năng, biên độ giảm dần theo thời gian. Ma sát càng lớn thì dao động tắt dần càng nhanh.
Chọn đáp án D
Câu 20:
Xem đáp án
+ Ta có: \[\Delta \ell = \frac{{mg}}{k} = \frac{g}{{{\omega ^2}}} \Rightarrow \omega = \sqrt {\frac{g}{{\Delta \ell }}} = \sqrt {\frac{{{\pi ^2}}}{{0,04}}} = 5\pi \left( {{\rm{rad/s}}} \right)\]
+ Chu kì dao động của con lắc là: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{5\pi }} = 0,4s\]
Chọn đáp án C
Câu 21:
Xem đáp án
Xét: \[\frac{{{O_1}M - {O_2}M}}{\lambda } = \frac{{3,25 - 9,25}}{4} = - 1,5\] M là điểm đứng yên.
\[\frac{{{O_1}N - {O_2}N}}{\lambda } = \frac{{33 - 67}}{4} = - 8,5\] N là điểm đứng yên.
Chọn đáp án D
Câu 22:
u = cos(20t - 4x) (cm) (x tính bằng mét, t tính bằng giây). Tốc độ truyền sóng trong môi trường trên bằng
Xem đáp án
+ Từ phương trình ta có:\[\left\{ \begin{array}{l}\omega = 20{\rm{rad/s}}\\\frac{{2\pi x}}{\lambda } = 4x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}f = \frac{{10}}{\pi }Hz\\\lambda = 0,5\pi \left( m \right)\end{array} \right.\]
+ Vận tốc truyền sóng là: \[v = \lambda .f = 0,5\pi .\frac{{10}}{\pi } = 5\left( {{\rm{m/s}}} \right)\]
Chọn đáp án D
Câu 23:
Xem đáp án
+ Có: \[\omega = \frac{{2\pi }}{T} = 2\pi \](rad/s)
+ Năng lượng dao động của vật là \[W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,5.{\left( {2\pi } \right)^2}.0,{02^2} = 0,004J\]
Chọn đáp án A
Câu 24:
Xem đáp án
+ Chu kì dao động của con lắc: \[T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow {T^2} \sim \ell \]
+ Khi \[\ell = {\ell _1} + {\ell _2} \Rightarrow {T^2} = T_1^2 + T_2^2 = {2^2} + 1,{5^2} = 6,25 \Rightarrow T = 2,5s\]
Chọn đáp án A
Câu 25:
x1= 3cos(4t) cm, x2= 3cos(4t +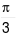 
) cm. Dao động tổng hợp của vật có phương trình
Xem đáp án
\[x = {x_1} + {x_2} = 3\angle 0 + 3\angle \frac{\pi }{3} = 3\sqrt 3 \angle \frac{\pi }{6}\]
Chọn đáp án B
Câu 26:
Xem đáp án
+ Có 5 nút sóng (kể cả A và B) Có 4 bụng sóng
+ Ta có, chiều dài của dây thỏa mãn:\[\ell = k\frac{\lambda }{2} = k\frac{v}{{2f}}\]
\[ \Rightarrow 1 = 4\frac{v}{{2.50}} \Rightarrow v = 25\left( {{\rm{m/s}}} \right)\]
Chọn đáp án D
Câu 27:
Xem đáp án
+ Có A = 5 cm, vmax= 10 cm/s ω = 2 (rad/s)
+ Chu kì dao động của vật nhỏ là: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1s\]
Chọn đáp án A
Câu 28:
Xem đáp án
+ Tần số góc của dao động: \[\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{50}}{{0,25}}} = 10\sqrt 2 \left( {{\rm{rad/s}}} \right)\]
+ Độ biến dạng của lò xo khi ở VTCB: \[\Delta \ell = \frac{{mg}}{k} = \frac{{0,25.10}}{{50}} = 0,05m = 5cm\]
+ Biên độ dao động của con lắc: \[{A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} \Rightarrow A = 0,05\sqrt 2 m = 5\sqrt 2 cm\]
+ Thời gian lò xo bị nén: tnén= \[\frac{2}{\omega }.arccos\left( {\frac{{\Delta \ell }}{A}} \right) = \frac{2}{{10\sqrt 2 }}.arccos\left( {\frac{5}{{5\sqrt 2 }}} \right) = \frac{{\pi \sqrt 2 }}{{40}}s\]
+ Tỉ số giữa thời gian lò xo bị nén và bị dãn trong một chu kì \[\left( {T = \frac{{2\pi }}{\omega } = \frac{{\pi \sqrt 2 }}{{10}}s} \right)\]là:
\[\frac{{{t_{nen}}}}{{{t_{dan}}}} = \frac{{{t_{nen}}}}{{T - {t_{nen}}}} = \frac{{\frac{{\pi \sqrt 2 }}{{40}}}}{{\frac{{\pi \sqrt 2 }}{{10}} - \frac{{\pi \sqrt 2 }}{{40}}}} = \frac{1}{3}\]
Chọn đáp án C
Câu 29:
Xem đáp án
+ Ta có: C thuộc cực tiểu thứ 2.
\[ \Rightarrow CA - CB = 2,5\lambda \Leftrightarrow 17 - 11 = 2,5\lambda \Rightarrow \lambda = 2,4cm\]
+ Số điểm dao động cực đại trên AC thỏa mãn: \[ - AB \le k\lambda \le CA - CB\]
\[ \Rightarrow - 18 \le 2,4k \le 6 \Leftrightarrow - 7,5 \le k \le 2,5\]
Vậy có 10 điểm dao động với biên độ cực đại trên AC, tương ứng với 10 đường dao động cực đại trên AC.
Chọn đáp án B
Câu 30:
Xem đáp án
+ Phương trình dao động của chất điểm có dạng: \[x = A\cos \left( {\omega t + \varphi } \right)\]
+ Chu kì dao động của chất điểm : \[T = \frac{t}{N} = \frac{{31,4}}{{100}} = \frac{\pi }{{10}}s\]
+ Tần số góc của dao động: \[\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\](rad/s)
+ Biên độ dao động của chất điểm:
\[{A^2} = {x^2} + {\left( {\frac{v}{\omega }} \right)^2} \Rightarrow A = \sqrt {0,{{02}^2} + \left( {\frac{{40\sqrt 3 {{.10}^{ - 2}}}}{{{{20}^2}}}} \right)} = 0,04m = 4cm\]
+ Tại t = 0, x = 2, v < 0 \[ \Rightarrow \varphi = \frac{\pi }{3}\]
Vậy phương trình dao động của vật là: \[x = 4\cos \left( {20t + \frac{\pi }{3}} \right)\](cm)
Chọn đáp án B