Đề thi Giữa kì 1 Vật lí 12 có đáp án (Đề 2)
-
1883 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
+ Mạch đang có tính dung kháng, nghĩa là\({Z_L} < {Z_C}\).
+ Khi tăng tần số của dòng điện thì \({Z_L}\)tăng và ZCgiảm.
Khi \(f = \frac{1}{{2\pi \sqrt {LC} }}\) ⇒ ZL= ZCthì trong mạch xảy ra cộng hưởng, hệ số công suất của mạch đạt cực đại là \(\cos \varphi = 1\).
Nếu tiếp tục tăng tần số thì ZL>ZC, khi này hệ số công suất của mạch giảm.
Chọn đáp án D
Câu 2:
 Xem đáp án
Xem đáp án
+ Phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
+ Phương trình vận tốc: \(v = x' = - A\omega \sin \left( {\omega t + \varphi } \right)\)
+ Phương trình gia tốc: \(a = v' = x'' = - A{\omega ^2}\cos \left( {\omega t + \varphi } \right)\)
+ Phương trình lực phục hồi: \[{F_{ph}} = ma = - mA{\omega ^2}\cos \left( {\omega t + \varphi } \right)\]
+ Động năng của vật dao động điều hòa: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{A^2}{\omega ^2}{\sin ^2}\left( {\omega t + \varphi } \right)\)
+ Thế năng của vật dao động điều hòa: \({W_t} = \frac{1}{2}m{\omega ^2}{x^2} = \frac{1}{2}m{\omega ^2}{A^2}{\cos ^2}\left( {\omega t + \varphi } \right)\)
+ Cơ năng dao động điều hòa: \(W = {W_d} + {W_t} = \frac{1}{2}m{\omega ^2}{A^2} = const\)
- Trong dao động điều hòa những đại lượng dao động cùng tần số với tần số li độ là
vận tốc, gia tốc và lực phục hồi.
- Động năng và thế năng dao động với tần số bằng 2 lần tần số li độ.
- Cơ năng không đổi theo thời gian.
Chọn đáp án C
Câu 3:
Một mạch điện xoay chiều AB gồm điện trở thuần \(R\), cuộn cảm thuần có độ tự cảm L thay đổi được, tụ điện có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }F\) mắc nối tiếp theo đúng thứ tự. Đặt vào hai đầu mạch điện một điện áp xoay chiều \(u = {U_0}c{\rm{os(100}}\pi {\rm{t}})V,\,t(s)\), \({U_0},\,\omega \), R có giá trị không đổi. Khi \(L = {L_1} = \frac{3}{\pi }H\) hoặc \(L = {L_2} = \frac{3}{{2\pi }}H\)thì điện áp hiệu dụng giữa hai đầu cuộn cảm thuần có cùng một giá trị. Tỉ số hệ số công suất của mạch khi \(L = {L_1}\) và khi \(L = {L_2}\) là
 Xem đáp án
Xem đáp án
+ \({Z_C} = 100\Omega ;{Z_{{L_1}}} = 300\Omega ;{Z_{{L_2}}} = 150\Omega \)
+ Với hai giá trị của L cho cùng điện áp hiệu dụng giữa hai đầu cuộn cảm, ta có:
\[\frac{1}{{{Z_{{L_1}}}}} + \frac{1}{{{Z_{{L_2}}}}} = \frac{{2{Z_C}}}{{{R^2} + Z_C^2}} \Leftrightarrow \frac{1}{{300}} + \frac{1}{{150}} = \frac{{2.100}}{{{R^2} + {{100}^2}}} \Rightarrow R = 100\Omega \]
+ Tỉ số hệ số công suất trong hai trường hợp:
\(\frac{{\cos {\varphi _1}}}{{\cos {\varphi _2}}} = \frac{{{Z_2}}}{{{Z_1}}} = \frac{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_C}} \right)}^2}} }}{{\sqrt {{R^2} + {{\left( {{Z_{{L_2}}} - {Z_C}} \right)}^2}} }} = \frac{{\sqrt {{{100}^2} + {{\left( {300 - 100} \right)}^2}} }}{{\sqrt {{{100}^2} + {{\left( {150 - 100} \right)}^2}} }} = \frac{1}{2}\)
Chọn đáp án B
Câu 4:
 Xem đáp án
Xem đáp án
Máy biến áp không có tác dụng biến đổi điện áp dòng điện một chiều, nên khi cho dòng điện không đổi qua cuộn sơ cấp của máy biến áp thì trong mạch kín của cuộn thứ cấp không có dòng điện chạy qua.
Chọn đáp án B
Câu 5:
 Xem đáp án
Xem đáp án
Chu kì dao động điều hòa: \(T = \frac{t}{N} = \frac{{24}}{{120}} = 0,2s \Rightarrow \omega = 10\pi \) rad/s.
Độ cứng của con lắc lò xo: \(k = m{\omega ^2} = 0,085.{\left( {10\pi } \right)^2} = 85{\rm{N/m}}\)
Chọn đáp án D
Câu 6:
 Xem đáp án
Xem đáp án
Ta có:\(\frac{{{v_{\max }}}}{v} = 4 \Rightarrow \frac{{A\omega }}{{\lambda .f}} = 4 \Leftrightarrow \lambda = \frac{{\pi A}}{2}\)
Chọn đáp án D
Câu 7:
Một vật dao động tắt dần chậm. Cứ sau mỗi chu kì, biên độ giảm 3%. Phần năng lượng của con lắc bị mất đi trong một dao động toàn phần là
 Xem đáp án
Xem đáp án
+ Biên độ dao động ban đầu là A0.
+ Cơ năng của vật lúc đầu: \({W_0} = \frac{1}{2}kA_0^2\)
+ Sau mỗi chu kì, biên độ giảm 3% nên biên độ dao động ở chu kì sau:
\(A = {A_0} - 0,03{A_0} = 0,97{A_0}\)
+ Cơ năng của con lắc ở chu kì sau:
\(W = \frac{1}{2}k{A^2} = \frac{1}{2}k.{\left( {0,97{A_0}} \right)^2} = 0,{97^2}.\frac{1}{2}kA_0^2 = 0,{97^2}{W_0}\)
+ Năng lượng của con lắc bị mất đi trong một dao động toàn phần:
\(\frac{{\Delta W}}{{{W_0}}} = \frac{{{W_0} - W}}{{{W_0}}}.100\% = \frac{{{W_0} - 0,{{97}^2}{W_0}}}{{{W_0}}}.100\% = 5,91\% \)
Chọn đáp án B
Câu 8:
 Xem đáp án
Xem đáp án
Khoảng cách giữa hai nút hay hai bụng sóng liên tiếp bằng một nửa bước sóng.
Chọn đáp án C
Câu 9:
Chọn phát biểu sai khi nói về dao động cơ.
 Xem đáp án
Xem đáp án
A – đúng.
B – sai, biên độ dao động cưỡng bức phụ thuộc vào tần số lực cưỡng bức.
C – đúng.
D – đúng.
Chọn đáp án B
Câu 10:
Một vật dao động điều hoà với phương trình x = 8cos(2t - \[\frac{\pi }{6}\]) cm. Vật đi qua vị trí có vận tốc v = - 8 cm/s lần thứ thứ 2015 vào thời điểm
 Xem đáp án
Xem đáp án
+ \({v_{\max }} = 16\pi \left( {{\rm{cm/s}}} \right)\)
+ Trong một chu kì, có 2 lần vật đi qua vị trí có vận tốc v = - 8 cm/s
+ Ta có: \({t_{2015}} = 1007T + {t_1}\) với t1là thời gian vật đi qua vị trí có vận tốc v = - 8 cm/s lần đầu tiên.
+ Tại thời điểm t = 0: \(x = 4\sqrt 3 ,v = \frac{{{v_{\max }}}}{2} = 8\pi >0\)
Sử dụng giản đồ vecto ta có:
+ Thời gian vật đi đến vị trí có vận tốc v = - 8 cm/s lần đầu tiên là:
\({t_1} = 2.\frac{T}{{12}} = \frac{T}{6}\)
Vậy \({t_{2015}} = 1007T + {t_1} = 1007T + \frac{T}{6} = \frac{{6043}}{6}\left( s \right)\)
Chọn đáp án B
Câu 11:
 Xem đáp án
Xem đáp án
+ \(i = 2\sin \left( {100\pi t + \frac{\pi }{6}} \right) = 2\cos \left( {100\pi t - \frac{\pi }{3}} \right)\)
+ Công suất tiêu thụ trên đoạn mạch bằng
\({\rm{P}} = UI\cos \varphi = \frac{{180}}{{\sqrt 2 }}.\frac{2}{{\sqrt 2 }}.\cos \left( { - \frac{\pi }{6} + \frac{\pi }{3}} \right) = 90\sqrt 3 W\)
Chọn đáp án B
Câu 12:
Đặt điện áp xoay chiều u=U0cost vào hai đầu đoạn mạch chỉ có tụ điện. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch, i, I0và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
 Xem đáp án
Xem đáp án
A – đúng
B – đúng
C – đúng
D – sai, u, i không thể cùng pha, mạch chỉ chứa tụ điện thì u vuông pha với i.
Chọn đáp án D
Câu 13:
 Xem đáp án
Xem đáp án
Từ phương trình ta có: \(\left\{ \begin{array}{l}\omega = 20\\\frac{{2\pi x}}{\lambda } = 4x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}f = \frac{{10}}{\pi }\left( {Hz} \right)\\\lambda = 0,5\pi \left( m \right)\end{array} \right.\)
Vận tốc truyền sóng là: \(v = \lambda .f = 0,5\pi .\frac{{10}}{\pi } = 5\left( {{\rm{m/s}}} \right)\)
Chọn đáp án C
Câu 14:
 Xem đáp án
Xem đáp án
+ Tần số, chu kì, tần số góc của li độ lần lượt là:
\(f = \frac{{f'}}{2} = \frac{{10}}{2} = 5Hz\),\(T = \frac{1}{f} = \frac{1}{5} = 0,2s\),\(\omega = 10\pi \) rad/s.
+ Tại thời điểm t = 0: \(x = \frac{A}{2},v >0\) tương ứng với \({W_d} = 3{W_t}\)
+ Tại thời điểm t = 0,05s: \(x = \frac{{A\sqrt 3 }}{2} \Rightarrow {W_t} = \frac{3}{4}W = 0,09375J\)
Chọn đáp án D
Câu 15:
 Xem đáp án
Xem đáp án
Suất điện động cảm ứng trong khung: \(e = - \Phi ' = {E_0}\cos \left( {\omega t} \right)\)
Biểu thức từ thông gửi qua khung dây là: \(\Phi = - \frac{{{E_0}}}{\omega }\sin \left( {\omega t} \right) = \frac{{{E_0}}}{\omega }\cos \left( {\omega t + \frac{\pi }{2}} \right)\)
Chọn đáp án D
Câu 16:
 Xem đáp án
Xem đáp án
Để con lắc đơn dao động điều hòa thì nó phải dao động với biên độ nhỏ và không có ma sát.
Chọn đáp án A
Câu 17:
 Xem đáp án
Xem đáp án
+ Ta có: \[\Delta {\rm{P}} = I.\Delta U \le 0,12{\rm{P}} \Rightarrow \Delta U \le 0,12.\frac{{\rm{P}}}{I}\](1)
+ Mà \({\rm{P}} = UI\cos \varphi = UI \Rightarrow \frac{{\rm{P}}}{I} = U\) (2)
+ Từ (1) và (2) \( \Rightarrow \Delta U \le 0,12.U = 0,12.100 = 12kV\)
Chọn đáp án B
Câu 18:
 Xem đáp án
Xem đáp án
+ Cảm kháng: \({Z_L} = 25\Omega \)
+ Tổng trở: \(Z = \sqrt {{{\left( {R + r} \right)}^2} + Z_L^2} = 25\sqrt 2 \Omega \)
+ \(\tan \varphi = \frac{{{Z_L}}}{{R + r}} = \frac{{25}}{{20 + 5}} = 1 \Rightarrow {\varphi _u} - {\varphi _i} = \frac{\pi }{4} \Rightarrow {\varphi _i} = - \frac{{3\pi }}{4}\)
+ Cường độ dòng điện cực đại: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{100\sqrt 2 }}{{25\sqrt 2 }} = 4A\)
⇒ Phương trình dòng điện: \(i = 4\cos \left( {100\pi t - \frac{{3\pi }}{4}} \right)\left( A \right)\)
Chọn đáp án A
Câu 19:
 Xem đáp án
Xem đáp án
+ Chu kì của con lắc trước khi được tích điện là: \(T = 2\pi \sqrt {\frac{\ell }{g}} \)
+ Sau khi quả cầu được tích điện, nó chịu tác dụng của lực điện trường có \({\vec F_d} \bot \vec P\)
+ Gia tốc trọng trường biểu kiến của con lắc sau khi được tích điện là:
\(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + {{\left( {\frac{{{F_d}}}{m}} \right)}^2}} = \sqrt {{g^2} + {{\left( {\frac{{q.E}}{m}} \right)}^2}} = \sqrt {9,{8^2} + {{\left( {\frac{{2\sqrt 5 {{.10}^{ - 7}}.4,{{9.10}^4}}}{{0,002}}} \right)}^2}} = 14,7\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)
+ Chu kì của con lắc sau khi được tích điện là: \(T' = 2\pi \sqrt {\frac{\ell }{{g'}}} \)
+ Lập tỉ số: \(\frac{T}{{T'}} = \sqrt {\frac{{g'}}{g}} = \sqrt {\frac{{14,7}}{{9,8}}} = \sqrt {1,5} \)
Chọn đáp án D
Câu 20:
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi và tần số f = 50 Hz vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM chi có cuộn cảm thuần \[L = \frac{{0,6}}{\pi }\] H, đoạn mạch MB gồm tụ điện C và điện trở \[R = 10\sqrt 3 \] Ω nối tiếp. Biết điện áp hai đầu đoạn mạch AB lệch pha \[\frac{{2\pi }}{3}\] so với điện áp hai đầu đoạn mạch MB. Điện dung của tụ điện bằng
 Xem đáp án
Xem đáp án
+ Cảm kháng: \({Z_L} = 60\Omega \)
+ Điện áp hai đầu đoạn mạch AB lệch pha \[\frac{{2\pi }}{3}\] so với điện áp hai đầu đoạn mạch MB nên \( \Rightarrow {Z_L} >{Z_C};{\rm{ }}{\varphi _{MB}} + {\varphi _{AB}} = \frac{{2\pi }}{3}\) (1)
+ Ta có: \(\tan {\varphi _{MB}} = \frac{{ - {Z_C}}}{R} = - \frac{{{Z_C}}}{{10\sqrt 3 }};{\rm{ }}\tan {\varphi _{AB}} = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{60 - {Z_C}}}{{10\sqrt 3 }}\) (2)
+ Từ (1) và (2) \( \Rightarrow C = \frac{{{{10}^{ - 3}}}}{{3\pi }}\left( F \right)\)
Chọn đáp án B
Câu 21:
 Xem đáp án
Xem đáp án
Hai đầu dây là cố định ta có:
\(\ell = \frac{{n\lambda }}{2} = \frac{{nv}}{{2f}} \Rightarrow f = \frac{{nv}}{{2\ell }}\)
Gọi 2 tần số liên tiếp có số bụng là n và n + 1, ta có:
\({f_{\left( {n + 1} \right)}} - {f_n} = \frac{{\left( {n + 1} \right)v}}{{2\ell }} - \frac{{nv}}{{2\ell }} = \frac{v}{{2\ell }} = {f_{\min }}\)
Vậy tần số nhỏ nhất tạo ra sóng dừng trên sợi dây là
fmin= f(n+1)– fn= 200 – 150 = 50 Hz
Chọn đáp án C
Câu 22:
 Xem đáp án
Xem đáp án
Ta có: \(\Delta L = {L_1} - {L_2} = 10\log \left( {\frac{{{I_1}}}{{{I_2}}}} \right)\)
Thay số vào ta được: \[{L_1} - {L_2} = 20 = 10\log \left( {\frac{{{{10}^{ - 3}}}}{{{I_2}}}} \right) \Rightarrow {I_2} = {10^{ - 5}}{\rm{W/}}{{\rm{m}}^{\rm{2}}}\]
Chọn đáp án A
Câu 23:
 Xem đáp án
Xem đáp án
+ Tại M: \({I_M} = \frac{1}{4}\left( {{I_A} + {I_B}} \right) = \frac{{25}}{{64}}{I_A} \Rightarrow \frac{{{I_A}}}{{{I_M}}} = \frac{{64}}{{25}}\)
+ Ta có: Cường độ âm tại một điểm cách nguồn âm khoảng r:
\(I = \frac{{\rm{P}}}{{4\pi {r^2}}} \Rightarrow I \sim \frac{1}{{{r^2}}}\)
+ Tỉ số: \(\frac{{{I_A}}}{{{I_M}}} = \frac{{64}}{{25}} \Rightarrow {\left( {\frac{{OM}}{{OA}}} \right)^2} = \frac{{64}}{{25}} \Rightarrow \frac{{OM}}{{OA}} = \frac{8}{5}\)
Chọn đáp án C
Câu 24:
 Xem đáp án
Xem đáp án
Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\frac{\ell }{g}} \Rightarrow {T^2} \sim \ell \)
Khi tăng chiều dài của con lắc thêm 25 cm, chu kì của con lắc lúc này tăng 0,2 s, suy ra:
\(\left\{ \begin{array}{l}T' = 2\pi \sqrt {\frac{{\ell + \Delta \ell }}{g}} \\T' = T + 0,2\end{array} \right. \Rightarrow 2\pi \sqrt {\frac{{\ell + \Delta \ell }}{g}} = 2\pi \sqrt {\frac{\ell }{g}} + 0,2 \Rightarrow \ell = 1,44\left( m \right)\)
Chọn đáp án A
Câu 25:
 Xem đáp án
Xem đáp án
+ Khoảng thời gian giữa hai lần liên tiếp vật có động năng bằng thế năng là: \(\Delta t = \frac{T}{4}\)
+ Tại thời điểm t và \(t + \Delta t\)ta có: \({x_1} \bot {x_2}\) hay \({v_1} \bot {v_2}\)
\[ \Rightarrow \left\{ \begin{array}{l}\frac{{\left| {{a_1}} \right|}}{{A{\omega ^2}}} = \frac{{\left| {{v_2}} \right|}}{{A\omega }}\\{\left( {A\omega } \right)^2} = v_1^2 + v_2^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\omega = \left| {\frac{{{a_1}}}{{{v_2}}}} \right|\\{\left( {A\omega } \right)^2} = v_1^2 + v_2^2\end{array} \right.\]
\[ \Rightarrow \left\{ \begin{array}{l}\omega = \left| {\frac{{22,5}}{{0,45\pi }}} \right| = \frac{{50}}{\pi }\left( {{\rm{rad/s}}} \right)\\{\left( {A.\frac{{50}}{\pi }} \right)^2} = {\left( {15\pi \sqrt 3 } \right)^2} + {\left( {45\pi } \right)^2}\end{array} \right. \Rightarrow A = 6\sqrt 3 \left( {cm} \right)\].
Chọn đáp án C
Câu 26:
 Xem đáp án
Xem đáp án
A – đúng
B – đúng
C – sai, năng lượng sóng là năng lượng dao động của các phần tử của môi trường có sóng truyền qua.
D – đúng
Chọn đáp án C
Câu 27:
 Xem đáp án
Xem đáp án
Vì hiệu điện thế giữa hai đầu cuộn dây lệch pha \[\frac{\pi }{2}\]so với hiệu điện thế giữa hai đầu đoạn mạch \( \Rightarrow \tan {\varphi _d}.\tan {\varphi _{AB}} = 1 \Leftrightarrow \frac{{{Z_L}}}{R}.\frac{{{Z_L} - {Z_C}}}{R} = 1 \Rightarrow {R^2} = {Z_L}.\left( {{Z_L} - {Z_C}} \right)\)
Chọn đáp án C
Câu 28:
Trong mạch điện xoay chiều chỉ có tụ điện, phát biểu không đúng là:
 Xem đáp án
Xem đáp án
A – đúng, tụ điện không tiêu thụ công suất.
B – đúng, tần số càng lớn thì dung kháng của tụ càng nhỏ, dòng điện càng dễ đi qua tụ.
C – sai, mạch chỉ chứa tụ điện thì điện áp luôn chậm pha \(\frac{\pi }{2}\) so với cường độ dòng điện.
D – đúng.
Chọn đáp án C
Câu 29:
 Xem đáp án
Xem đáp án
A – sai, sóng ngang là sóng có phương dao động vuông góc với phương truyền sóng.
B – đúng
C – đúng
D – đúng
Chọn đáp án A
Câu 30:
 Xem đáp án
Xem đáp án
+ Bước sóng: \(\lambda = 2cm\)
+ Độ lệch pha giữa O và M: \[\Delta \varphi = \frac{{2\pi .OM}}{\lambda } = \frac{{2\pi .100}}{2} = 100\pi \]
⇒ M và O luôn dao động cùng pha
Chọn đáp án A
Câu 31:
 Xem đáp án
Xem đáp án
Sử dụng nguyên hàm.
Biểu thức vận tốc: \(v = \int {adt} = \int {6\sin \left( {20t} \right)dt} = - \frac{6}{{20}}\cos \left( {20t} \right) = 0,3\cos \left( {20t + \pi } \right)\left( {{\rm{m/s}}} \right)\)
Chọn đáp án A
Câu 32:
 Xem đáp án
Xem đáp án
Khi sóng truyền đi từ môi trường này sang môi trường khác, tần số dao động không thay đổi.
Chọn đáp án D
Câu 33:
 Xem đáp án
Xem đáp án
Con lắc dao động với biên độ lớn nhất khi xảy ra cộng hưởng:
\({\omega _F} = {\omega _0} \Leftrightarrow {\omega _F} = \sqrt {\frac{k}{m}} \Leftrightarrow 10 = \sqrt {\frac{{36}}{m}} \Rightarrow m = 0,36kg\)
Chọn đáp án D
Câu 34:
 Xem đáp án
Xem đáp án
Phương trình dao động của điểm M:
\({u_M} = A\cos \left( {\frac{{2\pi }}{T}t - \frac{{2\pi .MO}}{\lambda }} \right) = A\cos \left( {\frac{{2\pi }}{T}t - \frac{{2\pi .\frac{\lambda }{3}}}{\lambda }} \right) = A\cos \left( {\frac{{2\pi }}{T}t - \frac{{2\pi }}{3}} \right)\)
Tại \(t = \frac{T}{2}:{u_M} = 2cm \Rightarrow A = 4cm\)
Chọn đáp án C
Câu 35:
 Xem đáp án
Xem đáp án
+ Khoảng thời gian ngắn nhất để vận tốc liên tiếp bằng 0 là \(\frac{T}{2}\)
\(\frac{T}{2} = {t_2} - {t_1} \Rightarrow T = 1,5s\)
+ Tốc độ trung bình trong khoảng thời gian đó:
\({v_{tb}} = \frac{{2A}}{{\frac{T}{2}}} \Leftrightarrow 16 = \frac{{4A}}{{1,5}} \Rightarrow A = 6cm\)
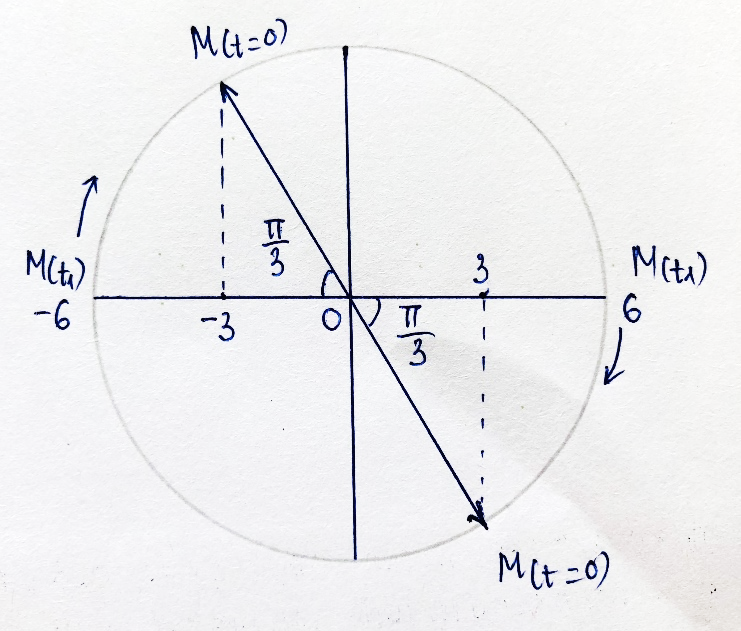
+ Tại \({t_1} = 3,25s = 2T + \frac{T}{6}\), vật đang ở biên.
Sử dụng đường tròn lượng giác, xác định được tại t = 0, chất điểm có
\(x = \frac{A}{2} = 3cm\)
Chọn đáp án D
Câu 36:
 Xem đáp án
Xem đáp án

Sử dụng đường tròn lượng giác.
Xác định được, vào thời điểm t + \[\frac{T}{6}\], li độ của vật là \(x = - 5{\rm{ }}cm\)
Chọn đáp án D
Câu 37:
 Xem đáp án
Xem đáp án
+ Chu kì: \(T = 0,02\left( s \right)\), có \(\frac{1}{{600}}\left( s \right) = \frac{T}{{12}}\)
\(\)
+ Sử dụng đường tròn lượng giác, ta được, tại \(t + \frac{1}{{600}}\left( s \right):u = \frac{{200\sqrt 2 .\sqrt 3 }}{2} = 100\sqrt 6 \left( V \right)\)
Chọn đáp án A
Câu 38:
 Xem đáp án
Xem đáp án
Sóng truyền trên một sợi dây có một đầu cố định, một đầu tự do. Điều kiện để có sóng dừng trên dây với chiều dài dây: \(\ell = \left( {2k + 1} \right)\frac{\lambda }{4}\)
Chọn đáp án B
Câu 39:
 Xem đáp án
Xem đáp án
+ Chiều dài của dây: \(\ell = k\frac{\lambda }{2}\)(k là số bụng sóng)
\( \Rightarrow f = \frac{{kv}}{{2\ell }} \Rightarrow \left( {f \sim k} \right)\)
+ Theo đầu bài ta có: \(\frac{f}{{f + 20}} = \frac{3}{5} \Rightarrow f = 30Hz\)
+ Để trên dây có 6 bụng sóng thì: \(\frac{f}{{f'}} = \frac{3}{6} \Rightarrow f' = 60Hz\)
Vậy cần tăng tần số thêm 10 Hz nữa.
Chọn đáp án A
Câu 40:
 Xem đáp án
Xem đáp án
+ Từ đề bài, có: \({S_1}{S_2} = 10\frac{\lambda }{2} = 10 \Rightarrow \lambda = 2\left( {{\rm{cm}}} \right)\)
+ Tần số dao động của hai nguồn: \(f = \frac{v}{\lambda } = \frac{{50}}{2} = 25\left( {Hz} \right)\)
Chọn đáp án D
