Tìm số phức z thỏa mãn (1-2i)z = 3 + i
A. z = 1 - i
B. z = 1 + i
C. z =
D. z =
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Ta có
![]()
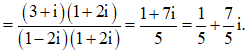
Gọi và là hai nghiệm phức của phương trình - 4z + 3 = 0. Giá trị của || + || bằng
Cho số phức z thỏa mãn điều kiện 3 |z-3i+1|5. Tập hợp các điểm biểu diễn của
Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
Cho hai số phức = 1 - 2i, = 3 + i. Tìm phần thực và ảo của số phức z =
Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.
Gọi là hai nghiệm phức của phương trình + 2z + 1 = 0. Tính P = .
Cho M(1;2) là điểm biểu diễn số phức z. Tìm tọa độ của điểm N biểu diễn số phức w = z + 2.
Cho số phức z = 3 - 2i. Tìm điểm biểu diễn của số phức w = z + i.
Xét các số phức z = a + bi(a,b) thỏa mãn điều kiện |z-4-3i| = . Tính P = a + b khi giá trị biểu thức |z+1-3i| + |z-1+i| đạt giá trị lớn nhất.