Viết giả thiết, kết luận cho định lí sau:
“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
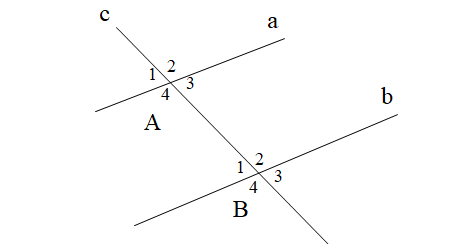
A.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\] là hai góc so le trong \[\widehat {{A_4}} = \widehat {{B_2}}\] |
Kết luận | a // b |
B.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đối đỉnh \[\widehat {{A_3}} = \widehat {{B_1}}\] |
Kết luận | a // b |
C.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc so le trong \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
Kết luận | a // b |
D.
Giả thiết | c cắt a tại A, c cắt b tại B \[\widehat {{A_3}}\] và \[\widehat {{B_1}}\] là hai góc đồng vị \[\widehat {{A_3}} \ne \widehat {{B_1}}\] |
Kết luận | a // b |
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
|
Giả thiết |
c cắt a tại A, c cắt b tại B \[\widehat {{A_4}}\] và \[\widehat {{B_2}}\] là hai góc so le trong \[\widehat {{A_4}} = \widehat {{B_2}}\] |
|
Kết luận |
a // b |
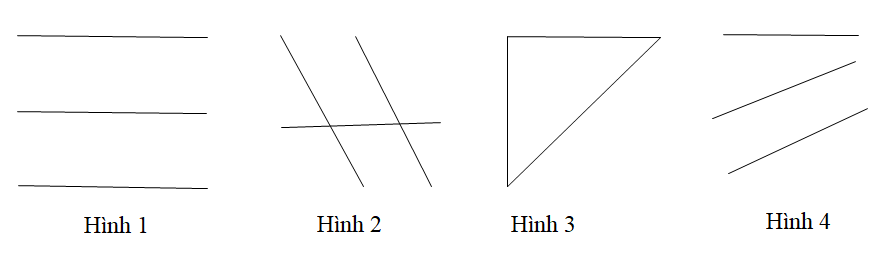
Trong định lý “Hai đường thẳng phân biệt cùng song song với một đường thứ ba thì chúng song song với nhau”, thì có
“Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
Hình vẽ minh hoạ cho định lí trên là:
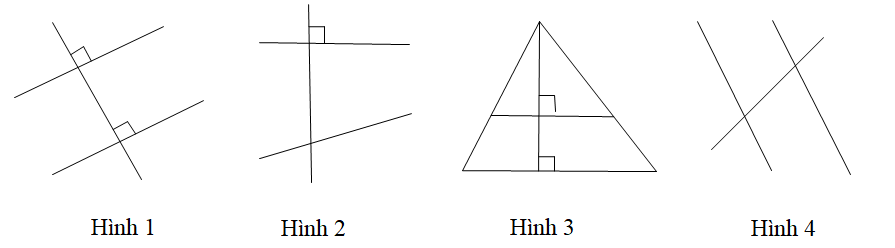
Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Hình vẽ minh hoạ cho định lí trên là:
Phát biểu định lí sau bằng lời.
Giả thiết | t cắt m tại A, t cắt n tại B \[\widehat {{A_1}}\] và \[\widehat {{B_1}}\]là hai góc đồng vị \[\widehat {{A_1}} = \widehat {{B_1}}\] |
Kết luận | m // n |
Điền vào chỗ trống những nội dung thích hợp để được định lí đúng.
Cho đoạn thẳng AB nếu M là trung điểm của AB thì ...
Điền vào chỗ trống nội dung thích hợp.
“Nếu Ot là tia phân giác của góc aOb thì….”
Chọn câu trả lời đúng.
Nếu một đường thẳng cắt hai đường thẳng song song thì …
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”
Hình minh họa nội dung định lí trên là