Cho \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù. Biết \[\widehat {mOn} = 124^\circ \] và Ot là tia phân giác của góc nOp. Số đo góc mOt là:
A. 152°;
B. 143°;
C. 45°;
D. 35°.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
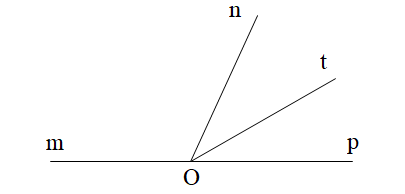
Vì \[\widehat {mOn}\] và \[\widehat {nOp}\] là hai góc kề bù nên \[\widehat {mOn} + \widehat {nOp} = 180^\circ \]
Suy ra \[\widehat {nOp} = 180^\circ - \widehat {mOn}\]
Hay \[\widehat {nOp} = 180^\circ - 124^\circ = 56^\circ \]
Mà \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2}\] (vì Ot là tia phân giác góc nOp)
Suy ra \[\widehat {nOt} = \widehat {tOp} = \frac{{\widehat {nOp}}}{2} = \frac{{56^\circ }}{2} = 28^\circ \]
Vì hai góc mOn và nOp là hai góc kề bù nên tia On nằm giữa hai tia Om và Op; tia Ot là phân giác của góc nOp nên tia Ot nằm giữa hai tia On và Op.
Do đó tia On nằm giữa hai tia Om và Ot.
Suy ra \[\widehat {mOt} = \widehat {mOn} + \widehat {nOt}\] suy ra \[\widehat {mOt} = 124^\circ + 28^\circ = 152^\circ \].
Do đó \[\widehat {mOt} = 152^\circ \].
Vậy chọn đáp án A.
Viết giả thiết, kết luận cho định lí sau:
“Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.”
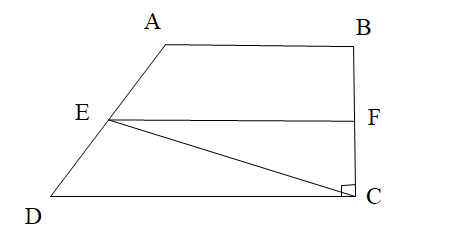
Cho hình vẽ. Tính góc FEC, biết EF // DC và \[\widehat {ECB} = 60^\circ \]:
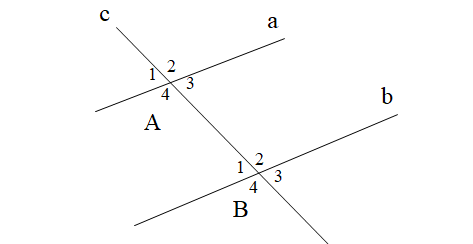
Cho các phát biểu sau:
(1) Tổng số đo hai góc kề nhau bằng 180o;
(2) Hai góc bằng nhau thì đối đỉnh;
(3) Hai đường thẳng song song thì cắt nhau;
(4) Hai góc kề bù có tổng số đo bằng 180o;
(5) Nếu NH = NK thì N là trung điểm của HK.
Có bao nhiêu phát biểu đúng?
Cho hình vẽ
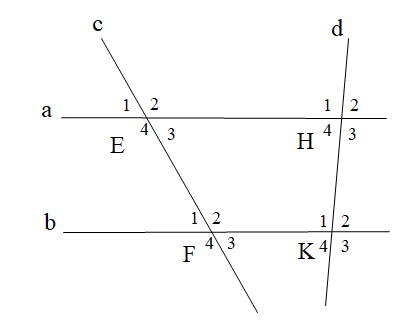
Biết a // b,
\[{\widehat E_1} = 48^\circ \]. Số đo \[\widehat {{F_3}}\] là:
Cho ba đường thẳng phân biệt a, b và c, biết c // a và c // b. Kết luận nào đúng:
Cho hình bình hành ABCD như hình vẽ. Biết IJ // DC và \[\widehat {JOC} = 34^\circ \].
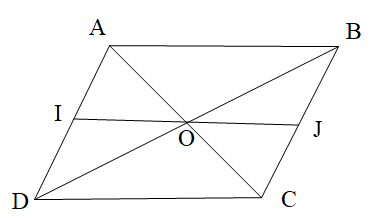
Số đo góc OCD là:
Cho định lí: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” và hình vẽ.
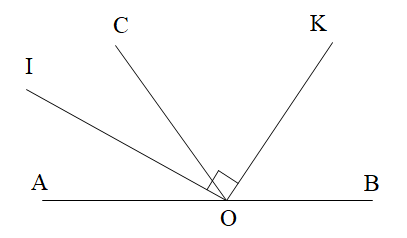
Kết luận của định lí là:
Biết một cặp góc so le trong \[\widehat {{A_4}}\; = \widehat {{B_2}} = 110^\circ \]. Tính số đo của cặp góc so le trong còn lại:
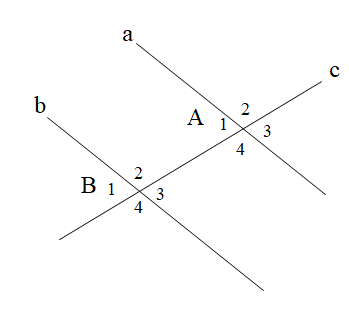
Cho hình vẽ,
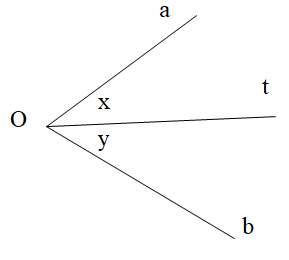
Biết \[\widehat {aOb} = 70^\circ \] và tia Ot là tia phân giác góc xOy. Tính x, y.
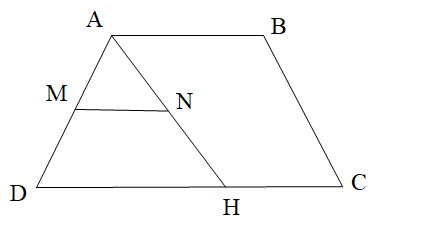
Cho hình thang ABCD như hình vẽ. Biết MN // DC, \[\widehat {DAB} = 120^\circ \] và \[\widehat {ANM} = 40^\circ \]. Số đo góc AHD là:
Cho góc MON và OI tia phân giác của góc đó. Vẽ tia phân giác OJ của góc NOI. Biết \[\widehat {IOJ} = 39^\circ \]. Số đo góc MON là: