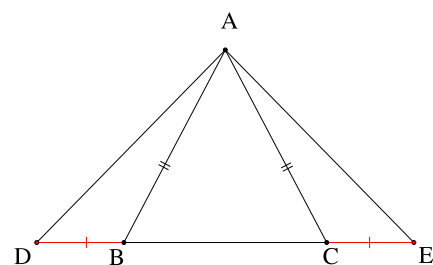
Cho hình vẽ dưới đây, biết tam giác ABC cân tại A và BD = CE. Khẳng định đúng là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
\(\Delta ABC\) cân tại A ⇒ \(\widehat {ABC} = \widehat {ACB}\) (tính chất)
Mà: \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) (hai góc kề bù
\(\widehat {ACB} + \widehat {ACE} = 180^\circ \) (hai góc kề bù)
⇒ \(\widehat {ABD} = \widehat {ACE}\)
Xét tam giác ADB và tam giác AEC có:
AB = AC (\(\Delta ABC\) cân tại A)
\(\widehat {ABD} = \widehat {ACE}\) (chứng minh trên)
BD = CE (theo giả thiết)
⇒ \(\Delta ADB = \Delta AEC\) (c.g.c)
⇒ AD = AE (hai cạnh tương ứng)
⇒ \(\Delta ADE\) cân tại A
Cho điểm D nằm trên đường trung trực của đoạn thẳng AB. Khẳng định đúng là
Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
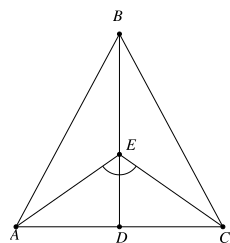
Cho hình vẽ dưới đây. Tam giác ABC cân tại B, D là trung điểm của AC. Biết \(\widehat {AEC} = 110^\circ \), tổng \(\widehat {ABE} + \widehat {BAE}\) là
Cho tam giác ABC có \(\widehat A = \widehat B\). Khẳng định đúng là
Cho điểm M thuộc đường trung trực của đoạn thẳng AB sao cho góc MAB bằng 60°. Khẳng định đúng nhất là
Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC.
Khẳng định đúng nhất là
Cho tam giác MNP cân tại M có \(\widehat P = 50^\circ \). Số đo góc M là
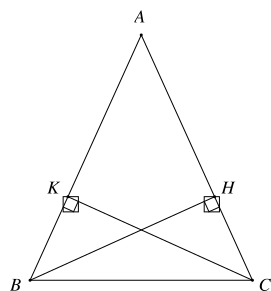
Cho hình vẽ dưới đây, biết tam giác ABC cân tại A. Khẳng định sai là
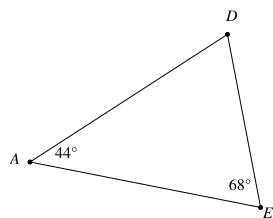
Cần thêm điều kiện gì để tam giác EAD trong hình vẽ dưới đây là tam giác cân:
Cho tam giác MNP cân tại M có MN = 6 cm; NP = 7 cm. Chu vi tam giác MNP là